题目内容
17. 如图,将长为4,宽为2的长方形ABCD绕顶点A顺时针旋转90°到达AB′C′D′,图中的两段弧线分别是顶点C、D经过的路径,则阴影部分的面积为4.(π取3)
如图,将长为4,宽为2的长方形ABCD绕顶点A顺时针旋转90°到达AB′C′D′,图中的两段弧线分别是顶点C、D经过的路径,则阴影部分的面积为4.(π取3)
分析 根据阴影部分的面积等于以C为半径的$\frac{1}{4}$圆的面积与半径为AD的$\frac{1}{4}$圆的面积之差,据此计算即可解答问题.
解答 解:∵四边形ABCD是矩形,
∴AC=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴阴影部分的面积$\frac{1}{4}$×3×(2$\sqrt{5}$)2-$\frac{1}{4}$×3×42
=4.
故答案为:4.
点评 本题考查了扇形的面积,矩形的性质,旋转的性质,解答此题的关键是明确阴影部分的面积包括哪几个部分.

练习册系列答案
相关题目
 如图,AC是?ABCD的对角线,点E、F在AC上,且四边形EBFD也是平行四边形,求证:AE=CF(思考不用全等的方法)
如图,AC是?ABCD的对角线,点E、F在AC上,且四边形EBFD也是平行四边形,求证:AE=CF(思考不用全等的方法)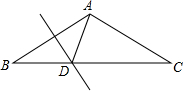 如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D.
如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D.
 B.
B.  C.
C.  D.
D. 