题目内容
19.如图,在等腰直角△AB中,∠BAC=90°,AB=AC,M是射线BC上一动点,N在射线AC上(点N,A不重合),满足MA=MN.(1)如图1,若∠AMN=45°,求证:BM=CN;
(2)当点M在射线BC上运动时,点N随之移动,过N作BC的垂线角射线BC于D.
①如图2,当点N在线段AC上时,试猜想线段MD与BC有何数量关系?写出你的结论并证明
②当点N在AC的延长线上时,①的结论是否仍然成立?请直接写出你的答案(不必证明).
(3)若BC=8,设BM的长为x,△MNC的面积为y,求y与x之间的关系式.
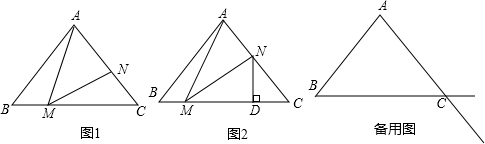
分析 (1)根据等腰直角三角形的性质得到∠B=∠C=45°,求得∠AMB=∠NMC,推出△ABM≌△CMN,根据全等三角形的性质即可得到结论;
(2)①如图2,过A作AE⊥BC于E,根据等腰直角三角形的性质得到AE=$\frac{1}{2}$BC,∠DNC=45°,证得∠AME=∠MND,推出△AME≌△MND,根据全等三角形的性质即可得到结论;②过A作AE⊥BC于E,根据等腰直角三角形的性质得到AE=$\frac{1}{2}$BC,∠DNC=45°,证得∠AME=∠MND,推出△AME≌△MND,根据全等三角形的性质即可得到结论;
(3)根据三角形的面积公式即可得到结论.
解答 解:(1)∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∵∠AMN=45°,
∴∠AMB=180°-45°-∠NMC,
∠CNM=180°-45°-∠NMC,
∴∠AMB=∠NMC,
在△ABM与△CNM中,$\left\{\begin{array}{l}{∠B=∠C}\\{∠AMB=∠CNM}\\{AM=MN}\end{array}\right.$,
∴△ABM≌△CMN,
∴BM=CN;
(2)①:如图2,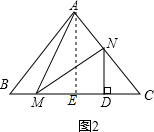 过A作AE⊥BC于E,
过A作AE⊥BC于E,
∵AB=AC,AE⊥BC,
∴AE=$\frac{1}{2}$BC,
∵ND⊥BC,
∵∠C=45°,
∴∠DNC=45°,
∴∠MND=180°-∠DNC-∠ANM=135°-∠ANM,
∵∠AMC=∠B+∠BAM=45°+90°-∠MAN=135°-∠MAN,
∵AM=MN,
∴∠MAN=∠ANM,
∴∠AME=∠MND,
在△AME与△MDN中,$\left\{\begin{array}{l}{∠AEM=∠MDN=90°}\\{∠AME=∠MND}\\{AM=MN}\end{array}\right.$,
∴△AME≌△MND,
∴MD=AE=$\frac{1}{2}$BC;
②:①的结论仍然成立;
过A作AE⊥BC于E,
∵AB=AC,AE⊥BC,
∴AE=$\frac{1}{2}$BC,
∵ND⊥BC,
∵∠ACB=45°,
∴∠DNC=45°,
∴∠MND=45°+∠ANM,
∵∠AMC=45°+∠MAN,
∵AM=MN,
∴∠MAN=∠ANM,
∴∠AME=∠MND,
在△AME与△MDN中,$\left\{\begin{array}{l}{∠AEM=∠MDN=90°}\\{∠AME=∠MND}\\{AM=MN}\end{array}\right.$,
∴△AME≌△MND,
∴MD=AE=$\frac{1}{2}$BC;
(3)∵BC=8,BM=x,
∴CM=8-x,或CM=x-8,
∵DN=CD,
∴DN=CM-DM=8-x-4=4-x,
∴y=$\frac{1}{2}$(8-x)(4-x)=-$\frac{1}{2}$x2-6x+16.或y=$\frac{1}{2}$(x-8)(4-x)=$\frac{1}{2}$x2+6x-16.
点评 不要看错了全等三角形的判定和性质,等腰直角三角形的性质,求函数的解析式,正确的作出辅助线是解题的关键.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案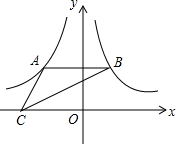 如图,AB平行于x轴,点A在反比例函数$y=-\frac{4}{x}$的图象上,点B在反比例函数$y=\frac{3}{x}$的图象上,点C在x轴上,则△ABC的面积为( )
如图,AB平行于x轴,点A在反比例函数$y=-\frac{4}{x}$的图象上,点B在反比例函数$y=\frac{3}{x}$的图象上,点C在x轴上,则△ABC的面积为( )| A. | $\frac{7}{3}$ | B. | 7 | C. | $\frac{7}{4}$ | D. | $\frac{7}{2}$ |
 C.
C.  D.
D. 

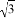 ,
,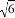 ,3,2
,3,2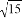 ,…,3
,…,3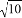 ,按下面的方法进行排列:
,按下面的方法进行排列:  ,
,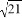 ,2
,2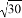 ;
; 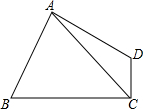 如图,四边形ABCD,∠BAD=∠BCD=90°,AB=AD.
如图,四边形ABCD,∠BAD=∠BCD=90°,AB=AD.
