题目内容
9.(1)(-5$\frac{1}{3}$)+3$\frac{5}{6}$;(2)$\frac{13}{5}$-($\frac{1}{6}$-0.4)+(-2.75-$\frac{1}{12}$);
(3)1$\frac{1}{3}$÷(-1$\frac{7}{9}$);
(4)-2.5÷(-$\frac{5}{8}$)×$\frac{1}{{3}^{2}}$÷(-$\frac{2}{3}$)2;
(5)2$\frac{1}{2}$÷(0.25-$\frac{2}{3}$+$\frac{1}{3}$);
(6)-14-(1-0.5)×$\frac{1}{3}$×[2-(-3)2].
分析 (1)利用加法法则计算即可;
(2)先化简,再分类计算即可;
(3)利用除法法则计算即可;
(4)先算乘方,再算乘除;
(5)先算括号里面的加减,再算除法;
(6)先算乘方和括号里面的运算,再算乘法,最后算减法.
解答 解:(1)原式=-1$\frac{1}{2}$;
(2)原式=$\frac{13}{5}$-$\frac{1}{6}$+0.4-2.75-$\frac{1}{12}$
=2.6+0.4-2.75-0.25
=0;
(3)原式=$\frac{4}{3}$×(-$\frac{9}{16}$)
=-$\frac{3}{4}$;
(4)原式=-2.5×(-$\frac{8}{5}$)×$\frac{1}{9}$×$\frac{9}{4}$
=1;
(5)原式=$\frac{5}{2}$×(-12)
=-30;
(6)原式=-1-$\frac{1}{2}$×$\frac{1}{3}$×[2-9]
=-1+$\frac{7}{6}$
=$\frac{1}{6}$.
点评 此题考查有理数的混合运算,掌握运算顺序与运算方法是解决问题的关键.

练习册系列答案
相关题目
20.在5,-$\frac{5}{7}$,0.56,-3,0.001,$\frac{12}{5}$这六个数中,分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个. |
18. 二次函数y=ax2+bx+c的部分对应值如下表:
二次函数y=ax2+bx+c的部分对应值如下表:
(1)求二次函数的解析式;
(2)直接写出二次函数的对称轴x=1,顶点坐标(1,-9),与x轴的交点(-2,0)、(4,0),与y轴的交点(0,-8);
(3)画出这个二次函数的图象,利用图象直接写出当x为何值时,y>0.
 二次函数y=ax2+bx+c的部分对应值如下表:
二次函数y=ax2+bx+c的部分对应值如下表:| x | … | -3 | -2 | 0 | 1 | 3 | 4 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 0 | 7 | … |
(2)直接写出二次函数的对称轴x=1,顶点坐标(1,-9),与x轴的交点(-2,0)、(4,0),与y轴的交点(0,-8);
(3)画出这个二次函数的图象,利用图象直接写出当x为何值时,y>0.
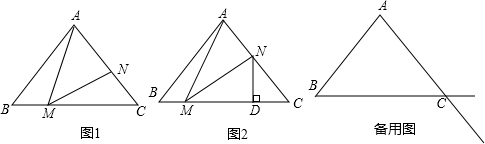
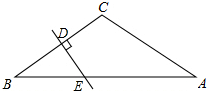 如图,在等腰△ABC中,∠BCA=120°,DE是AC的垂直平分线,线段DE=1cm,求BE的长.
如图,在等腰△ABC中,∠BCA=120°,DE是AC的垂直平分线,线段DE=1cm,求BE的长.