题目内容
13.已知一次函数y=-3x+4,则下列说法中不正确的是( )| A. | 该函数的图象经过点(1,1) | |
| B. | 该函数的图象不经过第三象限 | |
| C. | y的值随x的值的增大而减小 | |
| D. | 该函数的图象与x轴的交点坐标为(-$\frac{4}{3}$,0) |
分析 将x=1代入一次函数解析式求出y值即可得出A正确;由一次函数解析式结合一次函数系数与图象的关系即可得出B正确;由一次函数一次项系数k=-3<0即可得出C正确;将y=0代入一次函数解析式中求出x值即可得出D不正确.此题得解.
解答 解:A、令y=-3x+4中x=1,则y=1,
∴该函数的图象经过点(1,1),即A正确;
B、∵在y=-3x+4中k=-3<0,b=4>0,
∴该函数图象经过第一、二、四象限,即B正确;
C、∵在y=-3x+4中k=-3<0,
∴y的值随x的值的增大而减小,即C正确;
D、令y=-3x+4中y=0,则-3x+4=0,解得:x=$\frac{4}{3}$,
∴该函数的图象与x轴的交点坐标为($\frac{4}{3}$,0),即D不正确.
故选D.
点评 本题考查了一次函数的性质以及一次函数图象与系数的关系,解题的关键是逐条分析四个选项.本题属于基础题,难度不大,解决该题时,熟悉一次函数的性质、一次函数图象上点的坐标特征以及一次函数图象与系数的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.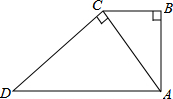 如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则
如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则
△ABC与△DCA的面积比为( )
 如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则
如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则△ABC与△DCA的面积比为( )
| A. | 2:3 | B. | 2:5 | C. | 4:9 | D. | $\sqrt{2}$:$\sqrt{3}$ |
5.关于反比例函数y=$\frac{2}{x}$的图象,下列说法正确的是( )
| A. | 图象经过点(1,1) | |
| B. | 当x<0时,y随x的增大而减小 | |
| C. | 图象的两个分支关于x轴成轴对称 | |
| D. | 图象的两个分支分布在第二、四象限 |
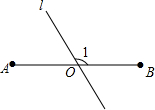 如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.
如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.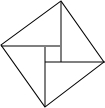 如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形的直角边分别为a、b,则ab的值是( )
如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形的直角边分别为a、b,则ab的值是( )