题目内容
5. 如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,若EF的长为6$\sqrt{3}$,求AB的长.
如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,若EF的长为6$\sqrt{3}$,求AB的长.
分析 首先证明四边形ABDE是平行四边形,AB=DE=CD,即D是CE的中点,在直角△CEF中利用三角函数即可求得到CE的长,则求得CD,进而根据AB=CD求解.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,
即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∵EF=6$\sqrt{3}$,
∴CF=6,
∴CE=2CF=12,
∴AB=6.
点评 本题考查了平行四边形的判定与性质,以及三角函数的应用,正确理解D是CE的中点是关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
15. 小敏不慎将一块矩形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的矩形玻璃,他带了两块碎玻璃,其编号应该是( )
小敏不慎将一块矩形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的矩形玻璃,他带了两块碎玻璃,其编号应该是( )
 小敏不慎将一块矩形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的矩形玻璃,他带了两块碎玻璃,其编号应该是( )
小敏不慎将一块矩形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的矩形玻璃,他带了两块碎玻璃,其编号应该是( )| A. | ①② | B. | ?①③ | C. | ③④ | D. | ?②④ |
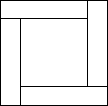 小明同学用四张长为x,宽为y的长方形卡片,拼出如图所示的包含两个正方形的图形(任意两张相邻的卡片之间没有重叠,没有空隙).
小明同学用四张长为x,宽为y的长方形卡片,拼出如图所示的包含两个正方形的图形(任意两张相邻的卡片之间没有重叠,没有空隙).