题目内容
阅读材料1:
对于两个正实数a,b,由于(
-
)2≥0,所以(
)2-2
•
+(
)2≥0,即a-2
+b≥0,所以得到a+b≥2
,并且当a=b时,a+b=2
.
阅读材料2:
若x>0,则
=
+
=x+
,因为x>0,
>0,所以由阅读材料1可得,x+
≥2
=2,即
的最小值是2,只有x=
时,即x=1时取得最小值.
根据以上阅读材料,请回答以下问题:
(1)比较大小:x2+1 2x(其中x≥1);x+
-2(其中x<-1)
(2)已知代数式
变形为x+n+
,求常数n的值;
(3)当x= 时,
有最小值,最小值为 .(直接写出答案)
对于两个正实数a,b,由于(
| a |
| b |
| a |
| a |
| b |
| b |
| ab |
| ab |
| ab |
阅读材料2:
若x>0,则
| x2+1 |
| x |
| x2 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
x•
|
| x2+1 |
| x |
| 1 |
| x |
根据以上阅读材料,请回答以下问题:
(1)比较大小:x2+1
| 1 |
| x |
(2)已知代数式
| x2+3x+3 |
| x+1 |
| 1 |
| x+1 |
(3)当x=
x+3+3
| ||
|
考点:分式的混合运算,二次根式的化简求值
专题:阅读型
分析:(1)x2+1-2x=(x-1)2≥0,所以x2+1≥2x;当x<-1时,由阅读材料1可得,-x-
>2
=2,所以x+
<-2;
(2)把代数式
变形为x+2+
,解答即可;
(3)当x=0 时,
有最小值,最小值为3.
| 1 |
| x |
(-x)•(-
|
| 1 |
| x |
(2)把代数式
| x2+3x+3 |
| x+1 |
| 1 |
| x+1 |
(3)当x=0 时,
x+3+3
| ||
|
解答:解:(1)x2+1-2x=(x-1)2≥0,所以x2+1≥2x;当x<-1时,由阅读材料1可得,-x-
>2
=2,所以x+
<-2;
(2)
=
=
+
+
=x+2+
=x+n+
,
所以n=2;
(3)当x=0 时,
有最小值,最小值为3.
故答案为:(1)≥<;(2)n=2;(3)0,3.
| 1 |
| x |
(-x)•(-
|
| 1 |
| x |
(2)
| x2+3x+3 |
| x+1 |
=
| x2+x+2x+2+1 |
| x+1 |
=
| x2+x |
| x+1 |
| 2x+2 |
| x+1 |
| 1 |
| x+1 |
=x+2+
| 1 |
| x+1 |
=x+n+
| 1 |
| x+1 |
所以n=2;
(3)当x=0 时,
x+3+3
| ||
|
故答案为:(1)≥<;(2)n=2;(3)0,3.
点评:本题主要考查了分式的混合运算.读懂材料并加以运用是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图,已知B、C、D三点在同一条直线上,∠B=∠1,2=∠E,根据这些条件你能判断AC∥ED吗?请说明你的理由.
如图,已知B、C、D三点在同一条直线上,∠B=∠1,2=∠E,根据这些条件你能判断AC∥ED吗?请说明你的理由.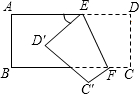 如图,小红把一个长方形纸片ABCD的一个角折了一次,EF为折痕.她问小华:“当我把纸条折成的∠EFB=40°,∠AEG等于多少度呢?”小华略加思索就给出了正确的答案;之后小华又反问:“如果要想让∠AEG是120°,你折的∠EFB应该是多少度?”请根据以上内容回答下列问题:
如图,小红把一个长方形纸片ABCD的一个角折了一次,EF为折痕.她问小华:“当我把纸条折成的∠EFB=40°,∠AEG等于多少度呢?”小华略加思索就给出了正确的答案;之后小华又反问:“如果要想让∠AEG是120°,你折的∠EFB应该是多少度?”请根据以上内容回答下列问题: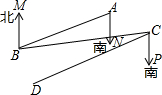 已知:如图B处在A处的南偏西60°方向,C处在B处的北偏东80°方向.
已知:如图B处在A处的南偏西60°方向,C处在B处的北偏东80°方向.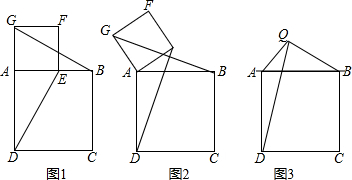
 如图,?ABCD中,点E是AD边的中点,BE交对角线AC于点F,若AF=2,则对角线AC长为
如图,?ABCD中,点E是AD边的中点,BE交对角线AC于点F,若AF=2,则对角线AC长为