题目内容
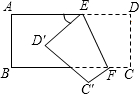 如图,小红把一个长方形纸片ABCD的一个角折了一次,EF为折痕.她问小华:“当我把纸条折成的∠EFB=40°,∠AEG等于多少度呢?”小华略加思索就给出了正确的答案;之后小华又反问:“如果要想让∠AEG是120°,你折的∠EFB应该是多少度?”请根据以上内容回答下列问题:
如图,小红把一个长方形纸片ABCD的一个角折了一次,EF为折痕.她问小华:“当我把纸条折成的∠EFB=40°,∠AEG等于多少度呢?”小华略加思索就给出了正确的答案;之后小华又反问:“如果要想让∠AEG是120°,你折的∠EFB应该是多少度?”请根据以上内容回答下列问题:(1)小华的正确答案是什么?他是怎么计算出来的?
(2)小红的正确答案是什么?说明理由.
考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:(1)由AD∥BC,根据平行线的性质,可求得∠DEF的度数,又由折叠的性质可得:∠GEF=∠DEF,即可求得∠DEG的度数,继而求得答案;
(2)由(1)知:∠DEG=2∠DEF=2∠EFB,∠DEG=180°-∠AEG,又由∠AEG是120°,即可求得答案.
(2)由(1)知:∠DEG=2∠DEF=2∠EFB,∠DEG=180°-∠AEG,又由∠AEG是120°,即可求得答案.
解答:解:(1)小华的正确答案是100°.
过程:∵AD∥BC,
∴∠DEF=∠EFB=40°,
由折叠的性质可得:∠GEF=∠DEF,
∴∠DEG=2∠DEF=80°,
∴∠AEG=180°-∠DEG=180°-80°=100°;
(2)小红的正确答案是30°.
理由:由(1)知:∠DEG=2∠DEF=2∠EFB,∠DEG=180°-∠AEG,
∵∠AEG=120°,
∴∠DEG=60°,
∴∠EFB=∠DEG=30°.
过程:∵AD∥BC,
∴∠DEF=∠EFB=40°,
由折叠的性质可得:∠GEF=∠DEF,
∴∠DEG=2∠DEF=80°,
∴∠AEG=180°-∠DEG=180°-80°=100°;
(2)小红的正确答案是30°.
理由:由(1)知:∠DEG=2∠DEF=2∠EFB,∠DEG=180°-∠AEG,
∵∠AEG=120°,
∴∠DEG=60°,
∴∠EFB=∠DEG=30°.
点评:此题考查了平行线的性质以及折叠的性质.此题难度适中,注意折叠中的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
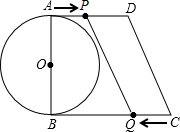 如图所示:在直角梯形ABCD中,AD∥BC,∠B=90°,AD=13cm,BC=16cm,CD=5cm,AB为⊙O的直径,动点P沿AD方向从点A开始向D以1cm/秒的速度运动,动点Q沿CB方向从点C开始向B以2cm/秒的速度运动,点P、Q分别从A、C两点同时出发,当其中一点停止时,另一点也随之停止运动.
如图所示:在直角梯形ABCD中,AD∥BC,∠B=90°,AD=13cm,BC=16cm,CD=5cm,AB为⊙O的直径,动点P沿AD方向从点A开始向D以1cm/秒的速度运动,动点Q沿CB方向从点C开始向B以2cm/秒的速度运动,点P、Q分别从A、C两点同时出发,当其中一点停止时,另一点也随之停止运动.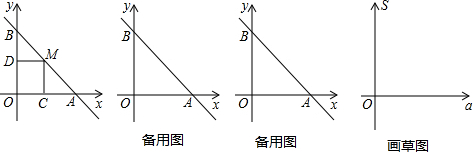
 如图,点A(0,3),B(0,-1),C是x轴上一点,且△ABC的面积为4,则点C的坐标为
如图,点A(0,3),B(0,-1),C是x轴上一点,且△ABC的面积为4,则点C的坐标为