题目内容
11.若关于x的分式方程$\frac{x+2a}{x-2}$=-1-$\frac{2}{2-x}$的解是正数,则a的取值范围是a<2且a≠0.分析 根据解分式方程的方法求出x的表达式,然后再根据条件求出a的范围.
解答 解:两边同乘(x-2)可得:x+2a=-(x-2)+2
x+2a=-x+4
2x=4-2a
x=2-a
由题意可知:$\left\{\begin{array}{l}{2-a>0}\\{2-a-2≠0}\end{array}\right.$
解得:a<2且a≠0
故答案为:a<2且a≠0
点评 本题考查分式方程的解法,涉及不等式的解法.

练习册系列答案
相关题目
2.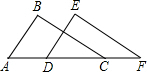 如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
 如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )| A. | ∠B=∠E | B. | ∠A=∠EDF | C. | ∠BCA=∠F | D. | BC∥EF |
6. 如图,长方体的长、宽、高分别为5、4、3,在下底面A处有一蚂蚁,它想吃到与它相对的上底面B处的食物,沿长方体侧面爬行的最短路程是( )
如图,长方体的长、宽、高分别为5、4、3,在下底面A处有一蚂蚁,它想吃到与它相对的上底面B处的食物,沿长方体侧面爬行的最短路程是( )
 如图,长方体的长、宽、高分别为5、4、3,在下底面A处有一蚂蚁,它想吃到与它相对的上底面B处的食物,沿长方体侧面爬行的最短路程是( )
如图,长方体的长、宽、高分别为5、4、3,在下底面A处有一蚂蚁,它想吃到与它相对的上底面B处的食物,沿长方体侧面爬行的最短路程是( )| A. | $\sqrt{74}$ | B. | 5$\sqrt{2}$ | C. | 4$\sqrt{5}$ | D. | 3$\sqrt{10}$ |
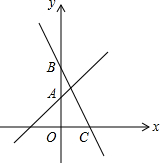 如图,已知函数y=x+2的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,4)且与x轴及y=x+2的图象分别交于点C、D,点D的坐标为($\frac{2}{3}$,n).
如图,已知函数y=x+2的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,4)且与x轴及y=x+2的图象分别交于点C、D,点D的坐标为($\frac{2}{3}$,n).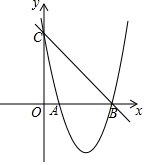 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).