题目内容
19.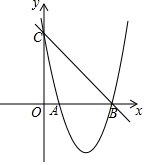 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,当平行四边形CBPQ的面积为30时,求点P的坐标.
分析 (1)根据待定系数法,可得函数解析式,
(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据二次函数的性质,可得答案;
(3)根据平行四边形的面积,可得BD的长,根据等腰直角三角形,可得E点坐标,根据待定系数法,可得PQ的解析式,根据解方程组,可得答案.
解答 解:(1)设直线BC的解析式为y=kx+m,将B(5,0),C(0,5)代入,得
$\left\{\begin{array}{l}{5k+m=0}\\{m=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{m=5}\end{array}\right.$.
∴直线BC的解析式为y=-x+5.
将B(5,0),C(0,5)代入y=x2+bx+c,得
$\left\{\begin{array}{l}{25+5b+c=0}\\{c=5}\end{array}\right.$,解得
$\left\{\begin{array}{l}{b=-6}\\{c=5}\end{array}\right.$.
∴抛物线的解析式y=x2-6x+5;
(2)∵点M是抛物线在x轴下方图象上的动点,
∴设M(m,m2-6m+5).
∵点N是直线BC上与点M横坐标相同的点,
∴N(m,m+5).
∵当点M在抛物线在x轴下方时,N的纵坐标总大于M的纵坐标.
∴MN=-m+5-(m2-6m+5)=-m2+5m=-(m-$\frac{5}{2}$)2+$\frac{25}{4}$.
∴MN的最大值是$\frac{25}{4}$.
(3)如图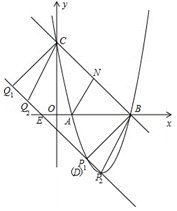 ,
,
设平行四边形CBPQ的边BC上的高为BD,则BC⊥BD,可求BC=5$\sqrt{2}$,
由平行四边形CBPQ的面积为30可得,BC×BD=30,从而BD=3$\sqrt{2}$.
设直线PQ交x轴于E点,
∵BC⊥BD,∠OBC=45°,
∴∠EBD=45°,△EBD为等腰直角三角形,BE=$\sqrt{2}$BD=6.
∵B(5,0),
∴E(-1,0).
设直线PQ的解析式为y=-x+s,将E点坐标代入函数解析式,得
0=-(-1)+s,
解得s=-1,
从而直线PQ的解析式为y=-x-1.
联立直线与抛物线,得
$\left\{\begin{array}{l}{y=-x-1}\\{y={x}^{2}-6x+5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=-4}\end{array}\right.$,
故点P的坐标为(2,-3),(3,-4).
点评 本题考察了二次函数综合题,(2)利用平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标得出二次函数是解题关键;(3)利用等腰直角三角形得出E点坐标是解题关键.

 53随堂测系列答案
53随堂测系列答案 下面说法,错误的是( )
下面说法,错误的是( )| A. | 一个平面截一个球,得到的截面一定是圆 | |
| B. | 一个平面截一个正方体,得到的截面可以是五边形 | |
| C. | 棱柱的截面不可能是圆 | |
| D. | 甲、乙两图中,只有乙才能折成正方体 |
| A. | (4x-3y)(-3y-4x) | B. | (2x2-y2)(2x2+y2) | C. | (a+b)(-b+a) | D. | (-x+y)(x-y) |
 有一半径为1m的圆形铁片,要从中剪出一个最大的圆心角为90°的扇形ABC,用来围成一个圆锥,该圆锥底面圆的半径是$\frac{\sqrt{2}}{4}$米.
有一半径为1m的圆形铁片,要从中剪出一个最大的圆心角为90°的扇形ABC,用来围成一个圆锥,该圆锥底面圆的半径是$\frac{\sqrt{2}}{4}$米. 如图,在半径为R的圆形钢板上,冲去半径为r的四个小圆,若R=8.9cm,r=0.55cm,请你应用所学知识用最简单的方法计算剩余部分面积.(结果保留π)
如图,在半径为R的圆形钢板上,冲去半径为r的四个小圆,若R=8.9cm,r=0.55cm,请你应用所学知识用最简单的方法计算剩余部分面积.(结果保留π)