题目内容
 如图,在Rt△ABC中,∠A=90°,AC=6,AB=8.动点D从点B出发沿线段BA方向以每秒2个单位长度的速度运动,到A点停止.过点D作DE∥BC交AC于点E.设动点D运动的时间为x秒.AE的长度为y.
如图,在Rt△ABC中,∠A=90°,AC=6,AB=8.动点D从点B出发沿线段BA方向以每秒2个单位长度的速度运动,到A点停止.过点D作DE∥BC交AC于点E.设动点D运动的时间为x秒.AE的长度为y.(1)请用含x的代数式直接表示线段BD和AD的长.
(2)求y与x之间的函数关系式.(不要求写自变量x的取值范围).
(3)若△BDE的面积为6,求x的值.
(4)当△BDE为等腰三角形时,求x的值.
考点:相似三角形的判定与性质
专题:
分析:(1)根据题意可求得含x的代数式的线段BD和AD的长;
(2)根据已知条件DE∥BC可以判定△ADE∽△ABC;然后利用相似三角形的对应边成比例求得
=
;最后用x、y表示该比例式中的线段的长度;
(3)根据∠A=90°得出S△BDE=
•BD•AE=6,再解一元二次方程即可得到x值;
(4)根据∠BDE=>90°判断出只有BD为腰长这一情况,利用相似三角形的性质可求得x.
(2)根据已知条件DE∥BC可以判定△ADE∽△ABC;然后利用相似三角形的对应边成比例求得
| AD |
| AB |
| AE |
| AC |
(3)根据∠A=90°得出S△BDE=
| 1 |
| 2 |
(4)根据∠BDE=>90°判断出只有BD为腰长这一情况,利用相似三角形的性质可求得x.
解答:解:(1)根据题意可得:
BD=2x,
AD=AB-BD=8-2x,
(2)∵DE∥BC
∴△ADE∽△ABC
∴
=
∴
=
8
∴y=-
x+6,
其中0<x≤4;
(3)根据题意可知,
∵∠A=90°
∴S△BDE=
•BD•AE=
•2x•y=-
x2+6x,
当S△BDE=6时,
即6=-
x2+6x,
解得:x=2.
(4)∵∠BDE=∠A+∠AED>90°,
∴当△BDE为等腰三角形时,∠BDE为腰长的夹角,
∴BD为腰长.
∴BD=DE,
∵△ADE∽△ABC
∴
=
即:
=
解得:x=
.
BD=2x,
AD=AB-BD=8-2x,
(2)∵DE∥BC
∴△ADE∽△ABC
∴
| AD |
| AB |
| AE |
| AC |
∴
| 8-2x |
| 8 |
| y |
| 6 |
∴y=-
| 3 |
| 2 |
其中0<x≤4;
(3)根据题意可知,
∵∠A=90°
∴S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当S△BDE=6时,
即6=-
| 3 |
| 2 |
解得:x=2.
(4)∵∠BDE=∠A+∠AED>90°,
∴当△BDE为等腰三角形时,∠BDE为腰长的夹角,
∴BD为腰长.
∴BD=DE,
∵△ADE∽△ABC
∴
| AD |
| DE |
| AB |
| BC |
即:
| 8-2x |
| 2x |
| 8 |
| 10 |
解得:x=
| 20 |
| 9 |
点评:本题主要考查相似三角形的判定与性质、三角形的面积及解一元二次方程,找到等量比是解题的关键.

练习册系列答案
相关题目
 如图,二次函数y=ax2+bx-b-1的图象与x轴有一个交点在0和1之间(不含0和1),则a的取值范围是
如图,二次函数y=ax2+bx-b-1的图象与x轴有一个交点在0和1之间(不含0和1),则a的取值范围是
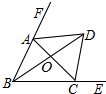 如图,△ABC中,BD平分∠ABC,CD平分∠ACE,下列结论:①点D到AB、BC、CA的距离相等;②CD∥BA;③S△AOB:S△COB=AB:BC=AO:OC;④∠FAD=∠DAC,其中正确的是( )
如图,△ABC中,BD平分∠ABC,CD平分∠ACE,下列结论:①点D到AB、BC、CA的距离相等;②CD∥BA;③S△AOB:S△COB=AB:BC=AO:OC;④∠FAD=∠DAC,其中正确的是( )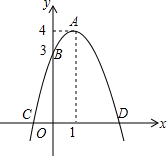 如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.
如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.