题目内容
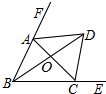 如图,△ABC中,BD平分∠ABC,CD平分∠ACE,下列结论:①点D到AB、BC、CA的距离相等;②CD∥BA;③S△AOB:S△COB=AB:BC=AO:OC;④∠FAD=∠DAC,其中正确的是( )
如图,△ABC中,BD平分∠ABC,CD平分∠ACE,下列结论:①点D到AB、BC、CA的距离相等;②CD∥BA;③S△AOB:S△COB=AB:BC=AO:OC;④∠FAD=∠DAC,其中正确的是( )| A、①②③④ | B、①③④ |
| C、①④ | D、②③④ |
考点:角平分线的性质,全等三角形的判定与性质
专题:
分析:过D作DN⊥BC于N,DZ⊥AC于Z,DM⊥BF于M,根据叫哦平分线性质得出DM=DN=DZ,即可判断①④,根据平行线的判定即可判断②,根据角平分线性质得出AB:BC=AO:OC,根据三角形面积公式求出后判断③即可.
解答:解: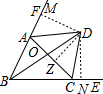
过D作DN⊥BC于N,DZ⊥AC于Z,DM⊥BF于M,
∵BD平分∠ABC,CD平分∠ACE,
∴DM=DN,DZ=DN,
∴DM=DN=DZ,
∴点D到AB、BC、CA的距离相等,∴①正确;
∵根据已知不能推出∠DCE=∠ABC,即不能推出CD∥AB,∴②错误;
∵BD平分∠ABC,
∴
=
,
设△ABC边AC上的高为h,
∴S△AOB:S△COB=(
AO×h):(
OC×h)=AO:OC=AB:BC,∴③正确;
∵DZ⊥AC于Z,DM⊥BF于M,DZ=DM,
∴∠FAD=∠DAC,∴④正确;
故选B.

过D作DN⊥BC于N,DZ⊥AC于Z,DM⊥BF于M,
∵BD平分∠ABC,CD平分∠ACE,
∴DM=DN,DZ=DN,
∴DM=DN=DZ,
∴点D到AB、BC、CA的距离相等,∴①正确;
∵根据已知不能推出∠DCE=∠ABC,即不能推出CD∥AB,∴②错误;
∵BD平分∠ABC,
∴
| AB |
| BC |
| AO |
| OC |
设△ABC边AC上的高为h,
∴S△AOB:S△COB=(
| 1 |
| 2 |
| 1 |
| 2 |
∵DZ⊥AC于Z,DM⊥BF于M,DZ=DM,
∴∠FAD=∠DAC,∴④正确;
故选B.
点评:本题考查了三角形的面积,角平分线性质的应用,注意:角平分线上的点到角的两边的距离相等,题目比较好,难度适中.

练习册系列答案
相关题目
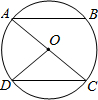
 点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )
点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )| A、2 | B、3 | C、4 | D、5 |
 如图,AC是⊙O的直径,AB,CD是⊙O的两条弦,且AB∥CD.如果∠BAC=32°,则∠AOD的度数是( )
如图,AC是⊙O的直径,AB,CD是⊙O的两条弦,且AB∥CD.如果∠BAC=32°,则∠AOD的度数是( )| A、16° | B、32° |
| C、48° | D、64° |
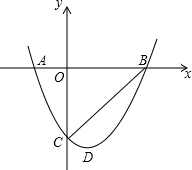 如图,已知抛物线y=x2-2x-3与x轴从左至右分别交于A、B两点,与y轴交于C点,顶点为D.
如图,已知抛物线y=x2-2x-3与x轴从左至右分别交于A、B两点,与y轴交于C点,顶点为D. 如图,在Rt△ABC中,∠A=90°,AC=6,AB=8.动点D从点B出发沿线段BA方向以每秒2个单位长度的速度运动,到A点停止.过点D作DE∥BC交AC于点E.设动点D运动的时间为x秒.AE的长度为y.
如图,在Rt△ABC中,∠A=90°,AC=6,AB=8.动点D从点B出发沿线段BA方向以每秒2个单位长度的速度运动,到A点停止.过点D作DE∥BC交AC于点E.设动点D运动的时间为x秒.AE的长度为y.