题目内容
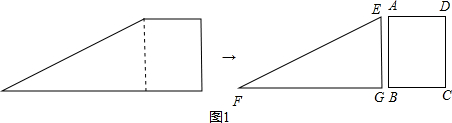
如图1.小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=5,AD=4.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2),请你求出AE和FG的长度;
(2)在(1)的条件下,小明先将三角形的边EG和矩形边AB重合,然后将△EFG沿直线BC向右平移,至F点与B重合时停止.在平移过程中,设G点平移的距离为x,两纸片重叠部分面积为y,求在平移的整个过程中,y与x的函数关系式,并求当重叠部分面积为10时,平移距离x的值(如图3).
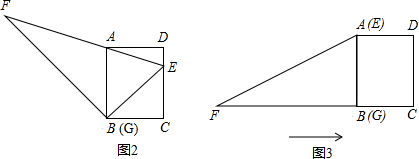

(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2),请你求出AE和FG的长度;
(2)在(1)的条件下,小明先将三角形的边EG和矩形边AB重合,然后将△EFG沿直线BC向右平移,至F点与B重合时停止.在平移过程中,设G点平移的距离为x,两纸片重叠部分面积为y,求在平移的整个过程中,y与x的函数关系式,并求当重叠部分面积为10时,平移距离x的值(如图3).
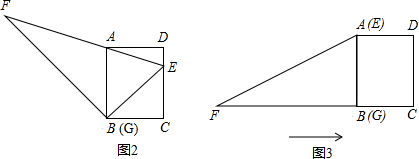
考点:几何变换综合题,勾股定理,平移的性质,旋转的性质,中心对称图形,相似三角形的性质,相似三角形的判定
专题:操作型
分析:(1)由题意易得CE=3,DE=2,AD=4,根据勾股定理即可求得AE的值,然后经过证明△EFG∽△AED,求得FG的值;
(2)分两种情况:①是x平移距离小于4时,②是x平移距离大于4时,分别求得解析式,把y=10分别代入两式,求得x的值,注意验证是否符合题意.
(2)分两种情况:①是x平移距离小于4时,②是x平移距离大于4时,分别求得解析式,把y=10分别代入两式,求得x的值,注意验证是否符合题意.
解答: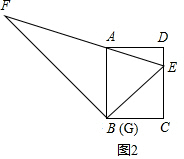 解:(1)∵AB=EG=DC=5,AD=BC=4,
解:(1)∵AB=EG=DC=5,AD=BC=4,
∴CE=
=
=3,DE=CD-CE=5-3=2,
∴AE=
=
=2
;
∵AB=EG,
∴∠BAE=∠BEA,
又∵∠BAE+∠EAD=90°,∠AED+∠EAD=90°,
∴∠BAE=∠AED
在△EFG和△AED中,∠BAE=∠AED,∠FBE=∠ADE=90°,
∴△EFG∽△AED,
那么,
=
,
∴FG=
=
=10;
(2)分两种情况:
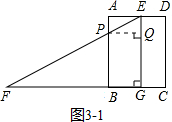 ①是x平移距离小于4时,如图3-1,EF与AB相交于P,过P作PQ⊥EG于Q点,
①是x平移距离小于4时,如图3-1,EF与AB相交于P,过P作PQ⊥EG于Q点,
∵△EFG的直角边FG=10,EG=5,
∴tanα=
=
=
,
∵∠FGE=90°,
∴PQ∥FC,四边形PQGB是矩形,
∴∠EPQ=∠F,
根据这个正切值,可求出相应的线段的数值,
得出,FB=FG-BG=10-x,BP=
=
,PQ=x,EQ=
,
∴重叠部分y=PB•BG+
BG•EQ=
+
x×
=-
x2+5x,
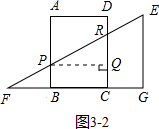 ②是x平移距离大于4时,如图3-2,EF与AB相交于P,与CD相交于R,
②是x平移距离大于4时,如图3-2,EF与AB相交于P,与CD相交于R,
∴y=PB•BC+
PQ•RQ=
+
×4×2=24-2x,
当重叠部分面积为10时,即y=10分别代入两等式,
-
x2+5x=10,
解得:x=10+2
(不合题意舍去)或x=10-2
,
y=24-2x=10得出,x=7,
∴当0≤x≤4时,y=-
x2+5x,
当4<x≤10时,y=-2x+24,
∴当y=10时,x=7或x=10-2
.
 解:(1)∵AB=EG=DC=5,AD=BC=4,
解:(1)∵AB=EG=DC=5,AD=BC=4,∴CE=
| BE2-BC2 |
| 52-42 |
∴AE=
| AD2+DE2 |
| 42+22 |
| 5 |
∵AB=EG,
∴∠BAE=∠BEA,
又∵∠BAE+∠EAD=90°,∠AED+∠EAD=90°,
∴∠BAE=∠AED
在△EFG和△AED中,∠BAE=∠AED,∠FBE=∠ADE=90°,
∴△EFG∽△AED,
那么,
| FG |
| EB |
| AD |
| DE |
∴FG=
| AD•EB |
| DE |
| 4×5 |
| 2 |
(2)分两种情况:
 ①是x平移距离小于4时,如图3-1,EF与AB相交于P,过P作PQ⊥EG于Q点,
①是x平移距离小于4时,如图3-1,EF与AB相交于P,过P作PQ⊥EG于Q点,∵△EFG的直角边FG=10,EG=5,
∴tanα=
| EG |
| FG |
| 5 |
| 10 |
| 1 |
| 2 |
∵∠FGE=90°,
∴PQ∥FC,四边形PQGB是矩形,
∴∠EPQ=∠F,
根据这个正切值,可求出相应的线段的数值,
得出,FB=FG-BG=10-x,BP=
| FB |
| 2 |
| 10-x |
| 2 |
| x |
| 2 |
∴重叠部分y=PB•BG+
| 1 |
| 2 |
| (10-x)x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 4 |
 ②是x平移距离大于4时,如图3-2,EF与AB相交于P,与CD相交于R,
②是x平移距离大于4时,如图3-2,EF与AB相交于P,与CD相交于R,∴y=PB•BC+
| 1 |
| 2 |
| 4(10-x) |
| 2 |
| 1 |
| 2 |
当重叠部分面积为10时,即y=10分别代入两等式,
-
| 1 |
| 4 |
解得:x=10+2
| 15 |
| 15 |
y=24-2x=10得出,x=7,
∴当0≤x≤4时,y=-
| 1 |
| 4 |
当4<x≤10时,y=-2x+24,
∴当y=10时,x=7或x=10-2
| 15 |
点评:本题以动态(平移和旋转)的形式考查了分类讨论的思想、函数的知识和直角三角形,具有很强的综合性.

练习册系列答案
相关题目
 点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )
点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )| A、2 | B、3 | C、4 | D、5 |
 如图,在Rt△ABC中,∠A=90°,AC=6,AB=8.动点D从点B出发沿线段BA方向以每秒2个单位长度的速度运动,到A点停止.过点D作DE∥BC交AC于点E.设动点D运动的时间为x秒.AE的长度为y.
如图,在Rt△ABC中,∠A=90°,AC=6,AB=8.动点D从点B出发沿线段BA方向以每秒2个单位长度的速度运动,到A点停止.过点D作DE∥BC交AC于点E.设动点D运动的时间为x秒.AE的长度为y.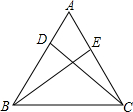 如图,若AB=AC,
如图,若AB=AC,