题目内容
 如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4
如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4| 2 |
(1)求新传送带AC的长度.
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.
参考数据:
| 2 |
| 3 |
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:(1)在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.
(2)通过解直角三角形,可求出BD、CD的长,进而可求出BC、PC的长.然后判断PC的值是否大于2米即可.
(2)通过解直角三角形,可求出BD、CD的长,进而可求出BC、PC的长.然后判断PC的值是否大于2米即可.
解答:解:(1)如图,
在Rt△ABD中,AD=ABsin45°=4
×
=4.
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=8.
即新传送带AC的长度约为8米;
(2)结论:货物MNQP不用挪走. (5分)
解:在Rt△ABD中,BD=ABcos45°=4
×
=4.
在Rt△ACD中,CD=ACcos30°=2
.
∴CB=CD-BD=2
-4≈0.9.
∵PC=PB-CB≈4-0.9=3.1>2,
∴货物MNQP不应挪走.
在Rt△ABD中,AD=ABsin45°=4
| 2 |
| ||
| 2 |
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=8.
即新传送带AC的长度约为8米;
(2)结论:货物MNQP不用挪走. (5分)
解:在Rt△ABD中,BD=ABcos45°=4
| 2 |
| ||
| 2 |
在Rt△ACD中,CD=ACcos30°=2
| 6 |
∴CB=CD-BD=2
| 6 |
∵PC=PB-CB≈4-0.9=3.1>2,
∴货物MNQP不应挪走.
点评:考查了坡度坡脚问题,应用问题尽管题型千变万化,但关键是设法化归为解直角三角形问题,必要时应添加辅助线,构造出直角三角形.在两个直角三角形有公共直角边时,先求出公共边的长是解答此类题的基本思路.

练习册系列答案
相关题目
 如图,在⊙O中,OD⊥BC,∠BOD=50°,则∠CAD的度数等于( )
如图,在⊙O中,OD⊥BC,∠BOD=50°,则∠CAD的度数等于( )| A、30° | B、25° |
| C、20° | D、15° |
在2.5,-2.5,0,2这四个数中,最小的一个数是( )
| A、2.5 | B、-2.5 | C、0 | D、2 |
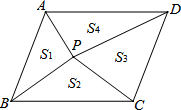 如图,点P是平行四边形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:
如图,点P是平行四边形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论: 如图,三个村庄A,B,C之间的距离分别为BC=5km,AC=12km,AB=13km.现准备从C村修一条公路CD直达公路AB,已知公路的造价为39000元/km,求修这条公路的最低造价是多少?
如图,三个村庄A,B,C之间的距离分别为BC=5km,AC=12km,AB=13km.现准备从C村修一条公路CD直达公路AB,已知公路的造价为39000元/km,求修这条公路的最低造价是多少? 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.
如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E. 如图,直线AB经过点A(0,-4),B(-1,0),与双曲线y=
如图,直线AB经过点A(0,-4),B(-1,0),与双曲线y=