题目内容
如图，在Rt△ABC中，∠B=90°，ED是AC的垂直平分线，交AC于点D，交BC于点E．（1）若∠BAE=20°，求∠C的度数．
（2）若AB=6，AC=10，求BE的长．
考点：线段垂直平分线的性质,勾股定理
专题：
分析：（1）由线段垂直平分线的性质可求得∠EAC=∠C，再结合三角形内角和定理可求得∠C；
（2）可先求得BC，设出BE，可表示出EC，又因为EC=EA，在Rt△ABE中可列出方程求得BE．
（2）可先求得BC，设出BE，可表示出EC，又因为EC=EA，在Rt△ABE中可列出方程求得BE．
解答：解：（1）∵ED是AC的垂直平分线，
∴EA=EC，
∴∠C=∠EAC，
∴∠CAB=∠EAC+20°=∠C+20°，
∵∠C+∠CAB=90°，
∴2∠C+20°=90°，
∴∠C=35°；
（2）∵AB=6，AC=10，
∴BC=8，
设BE=X，则AE=CE=8-X，
在Rt△ABE中，由勾股定理可得AE2=AB2+BE2，
即（8-X）2=62+X2，解得X=
∴BE=
．
∴EA=EC，
∴∠C=∠EAC，
∴∠CAB=∠EAC+20°=∠C+20°，
∵∠C+∠CAB=90°，
∴2∠C+20°=90°，
∴∠C=35°；
（2）∵AB=6，AC=10，
∴BC=8，
设BE=X，则AE=CE=8-X，
在Rt△ABE中，由勾股定理可得AE2=AB2+BE2，
即（8-X）2=62+X2，解得X=
| 7 |
| 4 |
∴BE=
| 7 |
| 4 |
点评：本题主要考查线段垂直平分线的性质，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键．
练习册系列答案
相关题目
点P（2，-1）在反比例函数y=
（k≠0）的图象上，则k的值是（ ）
| -k |
| x |
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
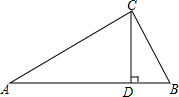如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．若AC=2，BC=1，则sin∠ACD=（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
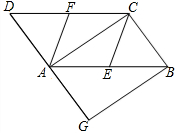如图，在?ABCD中，E、F分别为边AB、CD的中点，AC是对角线，过点B作BG∥AC交DA的延长线于点G．
如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°． 已知原传送带AB长为4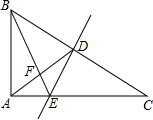
已知，如图，在Rt△ABC中，∠BAC=90°，BC的垂直平分线DE分别交BC、AC于点D、E，BE和AD相交于点F，设∠AFB=y，∠C=x．