题目内容
 如图,直线AB经过点A(0,-4),B(-1,0),与双曲线y=
如图,直线AB经过点A(0,-4),B(-1,0),与双曲线y=| m |
| x |
(1)求直线AB的解析式及m的值;
(2)试探究:在y轴上是否存在点M,使△ACM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
考点:反比例函数综合题
专题:
分析:(1)根据待定系数法即可求得直线AB的解析式,然后根据△AOC的面积为3,求得C的横坐标为-
,代入AB的解析式即可求得C的坐标,从而求得m的值.
(2)分两种情况分别讨论即可求得.
| 3 |
| 2 |
(2)分两种情况分别讨论即可求得.
解答:解:(1)∵直线AB经过点A(0,-4),B(-1,0),
∴设直线AB的解析式为y=kx+b,
∴
,解得
,
∴直线AB的解析式为y=-4x-4;
∵△AOC的面积为3,
∴
OA•|xC|=3,即
×4×|xC|=3,解得|xC|=
,
∴C的横坐标为-
,
代入y=-4x-4得,y=-4×(-
)-4=2,
∴C(-
,2),
∵双曲线y=
在第二象限与直线AB交于点C,
∴m=-3;
(2)设M(0,a),
当∠ACM=90°时,
∴△ACM∽△AOB,
∴
=
,
∵A(0,-4),B(-1,0),C(-
,2),
∴AB=
=
,AC=
=
,
∴
=
,解得a=
,
∴M(0,
);
当∠AMC=90°时,则△AMC∽△AOB,
∵C(-
,2),
∴M(0,2),
综上,在y轴上存在点M,使△ACM为直角三角形,M点的坐标为(0,
)或(0,2).
∴设直线AB的解析式为y=kx+b,
∴
|
|
∴直线AB的解析式为y=-4x-4;
∵△AOC的面积为3,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴C的横坐标为-
| 3 |
| 2 |
代入y=-4x-4得,y=-4×(-
| 3 |
| 2 |
∴C(-
| 3 |
| 2 |
∵双曲线y=
| m |
| x |
∴m=-3;
(2)设M(0,a),
当∠ACM=90°时,
∴△ACM∽△AOB,
∴
| AM |
| AB |
| AC |
| OA |
∵A(0,-4),B(-1,0),C(-
| 3 |
| 2 |
∴AB=
| 12+42 |
| 17 |
(
|
| 3 |
| 2 |
| 17 |
∴
| a+4 | ||
|
| ||||
| 4 |
| 19 |
| 8 |
∴M(0,
| 19 |
| 8 |
当∠AMC=90°时,则△AMC∽△AOB,
∵C(-
| 3 |
| 2 |
∴M(0,2),
综上,在y轴上存在点M,使△ACM为直角三角形,M点的坐标为(0,
| 19 |
| 8 |
点评:本题考查了反比例函数综合题:反比例函数与一次函数的交点坐标同时满足两个函数的解析式;运用待定系数法求函数的解析式以及使用分类讨论的思想方法解决数学问题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
下列四个多项式中,是x2-2x-8因式的为( )
| A、x+2 | B、x-2 |
| C、x+8 | D、x+4 |
式子
在实数范围内有意义,则x的取值范围是( )
| x+2 |
| A、x>-2 | B、x≥-2 |
| C、x<-2 | D、x≤-2 |
随着电子技术的不断进步,电子元件的尺寸大幅缩小,电脑芯片上某电子元件大约只有0.000 000 645mm2,这个数用科学记数法表示为( )
| A、6.45×10-7 |
| B、64.5×10-8 |
| C、0.645×10-6 |
| D、6.45×10-6 |
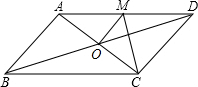 如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AO交AD于点M,若C△CDM=a,求C?ABCD.
如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AO交AD于点M,若C△CDM=a,求C?ABCD. 如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4
如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4