题目内容
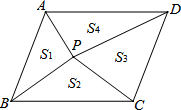 如图,点P是平行四边形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:
如图,点P是平行四边形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:①S1+S3=S2+S4;②若S3=S1,则S4=3S2;③若S1=S4,则S2=2S3;④若S1-S2=S3-S4,能判断P点一定在对角线BD上的正确结论的序号是
考点:平行四边形的性质
专题:
分析:分别设△PAB、△PBC、△PCD、△PDA的AB、BC、CD、AD边上的高为h、l、m、n,可分别表示出其面积,再结合平行四边形的性质依次判断即可.
解答:解:分别设△PAB、△PBC、△PCD、△PDA的AB、BC、CD、AD边上的高为h、l、m、n,设四边形ABCD的AB边上的高为o,BC边上的高为p,
则h+m=o,l+n=p,
∴S1=
AB•h,S2=
BC•l,S3=
CD•m,S4=
DA•n,
∵四边形ABCD为平行四边形,
∴AB=CD,BC=DA,且S四边形ABCD=AB•o=BC•p
∴S1+S3=S1=
AB•h+
CD•m=
AB•o,S2+S4=S1=
BC•l+
DA•n=
BC•p,
∴S1+S3=S2+S4,
故①正确;
若S3=S1,即
AB•h=
CD•m,且AB=CD,
∴h=m,即P点在o的中点,但在p的位置是不确定的,
∴S4=3S2不一定成立,
故②不正确;
当S1=S4时,由①可知S1+S3=S2+S4,
∴S3=S2,
故③不正确;
当S1-S2=S3-S4(1),且S1+S3=S2+S4(2),
(1)+(2)可得S1=S2,(1)-(2)可得S3=S4,
∴点P在BD上,
故④正确;
故答案为:①④.
则h+m=o,l+n=p,
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵四边形ABCD为平行四边形,
∴AB=CD,BC=DA,且S四边形ABCD=AB•o=BC•p
∴S1+S3=S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S1+S3=S2+S4,
故①正确;
若S3=S1,即
| 1 |
| 2 |
| 1 |
| 2 |
∴h=m,即P点在o的中点,但在p的位置是不确定的,
∴S4=3S2不一定成立,
故②不正确;
当S1=S4时,由①可知S1+S3=S2+S4,
∴S3=S2,
故③不正确;
当S1-S2=S3-S4(1),且S1+S3=S2+S4(2),
(1)+(2)可得S1=S2,(1)-(2)可得S3=S4,
∴点P在BD上,
故④正确;
故答案为:①④.
点评:本题主要考查平行四边形的性质和判定,掌握平行四边形的性质和判定是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边分别平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
点P(2,-1)在反比例函数y=
(k≠0)的图象上,则k的值是( )
| -k |
| x |
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
 如图,∠B=30°,∠ACE=35°,CE平分∠ACB,求∠A的度数.
如图,∠B=30°,∠ACE=35°,CE平分∠ACB,求∠A的度数. 指出图中∠A的同位角.∠B的内错角和同旁内角.
指出图中∠A的同位角.∠B的内错角和同旁内角. 如图所示,在△ABC中,底边BC=8cm,高AD=6cm,点E为AD上一动点,当点E从点D附近向点A运动时,△BEC的面积发生了变化
如图所示,在△ABC中,底边BC=8cm,高AD=6cm,点E为AD上一动点,当点E从点D附近向点A运动时,△BEC的面积发生了变化



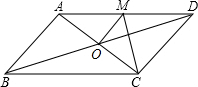 如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AO交AD于点M,若C△CDM=a,求C?ABCD.
如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AO交AD于点M,若C△CDM=a,求C?ABCD. 如图,已知:圆的两弦AB、CD相交于点P,AD、CB的延长线相交于圆外一点Q,∠AQC=36°,∠APC=80°.求∠ADC和∠BCD的度数.
如图,已知:圆的两弦AB、CD相交于点P,AD、CB的延长线相交于圆外一点Q,∠AQC=36°,∠APC=80°.求∠ADC和∠BCD的度数. 如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4
如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4