题目内容
10.?ABCD中,A(-1,0),B(3,0),D(0,3),直线y=kx-1,将?ABCD的面积分成两等分,求k的值.分析 连接AC、BD,交于点M,由平行四边形的性质得出M为BD的中点,得出点M的坐标,直线y=kx-1与y轴的交点是E,且坐标是(0,-1),若将矩形ABCD分成面积相等的两部分,则直线y=kx-1是过E与M的直线,再把M坐标代入直线y=kx-1,即可求出k的值.
解答 解:如图所示: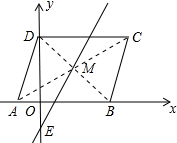
连接AC、BD,交于点M,
∵四边形ABCD是平行四边形,
∴MB=MD,
即M为BD的中点,
∵B(3,0),D(0,3),
∴点M的坐标为($\frac{3}{2}$,$\frac{3}{2}$);
设直线y=kx-1与y轴的交点是E,则坐标是(0,-1),
若将矩形ABCD分成面积相等的两部分,
则直线y=kx-1是过E与M的直线,分成的两部分是全等的梯形.
把点M($\frac{3}{2}$,$\frac{3}{2}$)代入得:$\frac{3}{2}$k-1=$\frac{3}{2}$,
解得:k=$\frac{5}{3}$.
点评 此题考查了一次函数的性质、平行四边形的性质、一次函数解析式的求法;解题的关键是确定直线y=kx-1是过E和M的直线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.我市某游乐场在暑假期间推出学生个人门票优惠活动,各类门票价格如下表:
某慈善单位欲购买三种类型的门票共100张奖励品学兼优的留守学生,设购买A种票x张,B种票张数是A种票的3倍还多7张,C种票y张,根据以上信息解答下列问题:
(1)直接写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买学生的夜场票不低于20张,且节假日通票至少购买5张,有哪几种购票方案?哪种方案费用最少?
| 票价种类 | (A)夜场票 | (B)日通票 | (C)节假日通票 |
| 单价(元) | 80 | 120 | 150 |
(1)直接写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买学生的夜场票不低于20张,且节假日通票至少购买5张,有哪几种购票方案?哪种方案费用最少?
19.若x-y=2,x-z=3,则(y-z)2-3(z-y)+9的值为( )
| A. | 13 | B. | 11 | C. | 5 | D. | 7 |
20.若A(2x-5,6-2x)在第四象限,则x的取值范围是( )
| A. | x>3 | B. | x>-3 | C. | x<-3 | D. | x<3 |
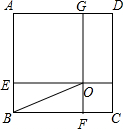 如图,在正方形ABCD中,点E、F、G、H分别在四边上,EH∥BC,GF∥AB,EH与FG交于点O,且AE=AG,若AE比CH长2,△BOF的面积为$\frac{3}{2}$
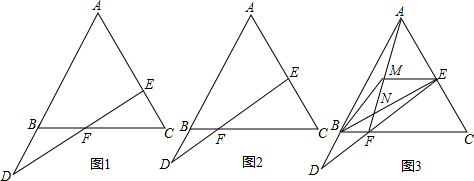
如图,在正方形ABCD中,点E、F、G、H分别在四边上,EH∥BC,GF∥AB,EH与FG交于点O,且AE=AG,若AE比CH长2,△BOF的面积为$\frac{3}{2}$ 如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB.
如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB. 三个大小相同的球恰好放在一个圆柱体盒子里,三个球的体积之和占整个盒子容积的几分之几.(V球=$\frac{4}{3}π{r^3}$)
三个大小相同的球恰好放在一个圆柱体盒子里,三个球的体积之和占整个盒子容积的几分之几.(V球=$\frac{4}{3}π{r^3}$)