题目内容
18.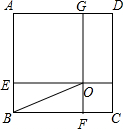 如图,在正方形ABCD中,点E、F、G、H分别在四边上,EH∥BC,GF∥AB,EH与FG交于点O,且AE=AG,若AE比CH长2,△BOF的面积为$\frac{3}{2}$
如图,在正方形ABCD中,点E、F、G、H分别在四边上,EH∥BC,GF∥AB,EH与FG交于点O,且AE=AG,若AE比CH长2,△BOF的面积为$\frac{3}{2}$(1)求正方形ABCD的面积;
(2)设AE=a,BE=b,求代数式a4+b4的值.
分析 (1)根据四边形ABCD是正方形,得到AD∥BC,AD=BC,AB∥CD,AB=CD,由于EH∥BC,GF∥AB,得出四边形AEOG是正方形,四边形AEHD,EBFO,GOHD是矩形,根据△BOF的面积为$\frac{3}{2}$,得到矩形EBFO的面积=3,设AE=OE=DH=x,BE=CH=y,列出$\left\{\begin{array}{l}{x-y=2}\\{xy=3}\end{array}\right.$,即可得到结果;
(2)由(1)求得AE=3,BE=1,代入即可得到结果.
解答 解:(1)∵ 四边形ABCD是正方形,
四边形ABCD是正方形,
∴AD∥BC,AD=BC,AB∥CD,AB=CD,
∵EH∥BC,GF∥AB,
∴四边形AEOG是正方形,四边形AEHD,EBFO,GOHD是矩形,
∴AE=DH,BE=CH,
∵△BOF的面积为$\frac{3}{2}$,
∴矩形EBFO的面积=3,
设AE=OE=DH=x,BE=CH=y,
∴$\left\{\begin{array}{l}{x-y=2}\\{xy=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
∴AEE=3,BE=1,
∴AB=AE+BE=4,
∴正方形ABCD的面积=4×4=16;
(2)由(1)求得AE=3,BE=1,
∴a=3,b=1,
∴a4+b4=34+11=82.
点评 本题考查了正方形的判定和性质,正方形的面积,三角形的面积,充分利用已知条件列方程组求出各线段是解题的关键.

练习册系列答案
相关题目
6.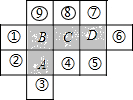 如图,标有数字①~⑨的正方形与标有字母A,B,C,D的正方形大小均相同.现从标有数字的9个正方形中等可能的任选一个,则所选正方形与标有字母的正方形所组成的图形恰可以是一个无盖的正方体的表面展开图,且没有盖的一面恰好与标有字母“A”的一面相对的概率为 ( )
如图,标有数字①~⑨的正方形与标有字母A,B,C,D的正方形大小均相同.现从标有数字的9个正方形中等可能的任选一个,则所选正方形与标有字母的正方形所组成的图形恰可以是一个无盖的正方体的表面展开图,且没有盖的一面恰好与标有字母“A”的一面相对的概率为 ( )
 如图,标有数字①~⑨的正方形与标有字母A,B,C,D的正方形大小均相同.现从标有数字的9个正方形中等可能的任选一个,则所选正方形与标有字母的正方形所组成的图形恰可以是一个无盖的正方体的表面展开图,且没有盖的一面恰好与标有字母“A”的一面相对的概率为 ( )
如图,标有数字①~⑨的正方形与标有字母A,B,C,D的正方形大小均相同.现从标有数字的9个正方形中等可能的任选一个,则所选正方形与标有字母的正方形所组成的图形恰可以是一个无盖的正方体的表面展开图,且没有盖的一面恰好与标有字母“A”的一面相对的概率为 ( )| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{2}$ |
3.我市政府为响应党中央建设社会主义新农村和节约型社会的号召,决定资助部分农村地区修建一批沼气池,使农民用到经济、环保的沼气能源.红星村共有264户村民,村里得到34万元的政府资助款,不足部分由村民集资解决.修建A型、B型沼气池共20个.两种型号沼气池每个修建费用、可供使用的户数、修建用地情况见下表:
政府土地部门只批给该村沼气池修建用地708m2.若修建A型沼气池x个,修建两种型号沼气池共需费用y万元.
(1)求y与x之间的函数关系式;
(2)既不超过政府批给修建沼气池用地面积,又要使该村每户村民用上沼气的修建方案有几种?
(3)若平均每户村民集资700元,能否满足所需费用最少的修建方案?
| 沼气池 | 修建费用(万元/个) | 可供使用户数(户/个) | 占地面积(m2/个) |
| A型 | 3 | 20 | 48 |
| B型 | 2 | 3 | 6 |
(1)求y与x之间的函数关系式;
(2)既不超过政府批给修建沼气池用地面积,又要使该村每户村民用上沼气的修建方案有几种?
(3)若平均每户村民集资700元,能否满足所需费用最少的修建方案?
7.已知3x=4y,则$\frac{x}{y}$的值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{7}$ | D. | $\frac{3}{7}$ |
8.若反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象过点(3,-4),则下列各点中也在该图象上的点是( )
| A. | (2,6) | B. | (-6,-2) | C. | (-3,4) | D. | (-3,-4) |
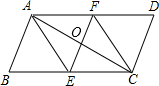 如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,分别交BC,AD于点E,F,连接AC,EF相交于点O.若点E是BC的中点,AB⊥AC,AB=2,则四边形AECF的面积是2$\sqrt{3}$.
如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,分别交BC,AD于点E,F,连接AC,EF相交于点O.若点E是BC的中点,AB⊥AC,AB=2,则四边形AECF的面积是2$\sqrt{3}$.