题目内容
11.已知菱形两条对角线的长分别为12和16,则这个菱形的周长为40,面积为96.分析 如图四边形ABCD是菱形,AC=12,BD=16,利用菱形的性质先求出AB,根据菱形的面积公式即可解决问题.
解答 解:如图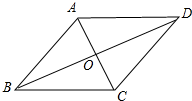 四边形ABCD是菱形,AC=12,BD=16,
四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,AO=$\frac{1}{2}$AC=6,BO=$\frac{1}{2}$BD=8,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴菱形的周长为40,菱形的面积为$\frac{1}{2}$×12×16=96.
故答案分别为40,96.
点评 本题考查菱形的性质、解题的关键是记住菱形的面积公式,记住菱形的对角线互相垂直,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.菱形的周长为20cm,两个相邻的内角的度数之比为1:2,则较长的对角线的长度是( )
| A. | 20$\sqrt{3}$ | B. | 5$\sqrt{3}$cm | C. | $\frac{5}{2}$$\sqrt{3}$cm | D. | 5cm |
20.已知菱形的周长为40cm,两条对角线之比3:4,则菱形面积为( )
| A. | 96cm2 | B. | 48cm2 | C. | 24cm2 | D. | 12cm2 |
1.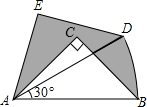 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为BD,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为BD,则图中阴影部分的面积是( )
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为BD,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为BD,则图中阴影部分的面积是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
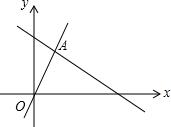 如图,函数y=2x和y=ax+4的图象相交于点A($\frac{3}{2},3$),则不等式2x>ax+4的解集为x>$\frac{3}{2}$.
如图,函数y=2x和y=ax+4的图象相交于点A($\frac{3}{2},3$),则不等式2x>ax+4的解集为x>$\frac{3}{2}$.