题目内容
1.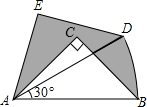 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为BD,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为BD,则图中阴影部分的面积是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
分析 先根据勾股定理得到AB=$\sqrt{2}$,再根据扇形的面积公式计算出S扇形ABD,由旋转的性质得到Rt△ADE≌Rt△ACB,于是S阴影部分=S△ADE+S扇形ABD-S△ABC=S扇形ABD.
解答 解:∵∠ACB=90°,AC=BC=1,
∴AB=$\sqrt{2}$,
∴S扇形ABD=$\frac{30π(\sqrt{2})^{2}}{360}$=$\frac{π}{6}$.
又∵Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,
∴Rt△ADE≌Rt△ACB,
∴S阴影部分=S△ADE+S扇形ABD-S△ABC=S扇形ABD=$\frac{π}{6}$.
故选:A.
点评 本题主要考查的是旋转的性质、扇形的面积公式,勾股定理的应用,将阴影部分的面积转化为扇形ABD的面积是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.据了解,2012年某县城商品房房价均价为7530元/平方米,2014年同期达到8120元/平方米,假设这两年无锡市房价的平均增长率为x,根据题意,所列方程为( )
| A. | 7530(1-x)2=8120 | B. | 7530x2=8120 | C. | 8120(1+x)2=7530 | D. | 7530(1+x)2=8120 |
6.若点(3,4)是反比例函数y=$\frac{2m-2}{x}$图象上一点,则此函数图象必须经过点( )
| A. | (2,6) | B. | (2,-6) | C. | (4,-3) | D. | (3,-4) |
13.以下问题,不适合用全面调查的是( )
| A. | 了解班上每位同学穿鞋的尺码 | |
| B. | 了解一个社区所有家庭的年收入 | |
| C. | 一批电视机的使用寿命 | |
| D. | 了解全校学生最喜爱的体育运动项目 |
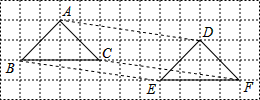 如图,△ABC平移到△DEF的位置,则下列说法:
如图,△ABC平移到△DEF的位置,则下列说法: 已知一次函数y=2x+4
已知一次函数y=2x+4