题目内容
16.等腰三角形的顶角是n°,那么它在一腰上的高与底边的夹角等于$\frac{n°}{2}$.分析 从已知条件结合图形,根据三角形的内角和定理以及等腰三角形的两个底角相等,得它的两个底角是$\frac{180°-n°}{2}$,再根据直角三角形的两个锐角互余,可得答案.
解答 解:∵等腰三角形的顶角是n°,
∴底角是$\frac{180°-n°}{2}$,
∴它的一腰上的高与底边的夹角=90°-$\frac{180°-n°}{2}$=$\frac{n°}{2}$.
故答案为:$\frac{n°}{2}$.
点评 此题主要考查了三角形的内角和定理以及等腰三角形的性质;题目比较简单,思路直接,属于基础题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
6.x是9的平方根,y是64的立方根,则x+y的值为( )
| A. | 3 | B. | 7 | C. | 3,7 | D. | 1,7 |
8.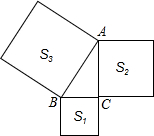 如图,在直角三角形ABC的三边上,向外做三个正方形,其中两个的面积为S3=169,S2=144,则另一个面积S1为( )
如图,在直角三角形ABC的三边上,向外做三个正方形,其中两个的面积为S3=169,S2=144,则另一个面积S1为( )
 如图,在直角三角形ABC的三边上,向外做三个正方形,其中两个的面积为S3=169,S2=144,则另一个面积S1为( )
如图,在直角三角形ABC的三边上,向外做三个正方形,其中两个的面积为S3=169,S2=144,则另一个面积S1为( )| A. | 50 | B. | 30 | C. | 25 | D. | 100 |
5.甲、乙两个仓库共存粮450吨,现从甲仓库运出存粮的60%,从乙仓库运出存粮的40%.结果乙仓库所余的粮食比甲仓库所余的粮食多30吨.若设甲仓库原来存粮x吨,乙仓库原来存粮y吨,则下列所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=450}\\{(1-60%)x-(1-40%)y=30}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=450}\\{60%x-40%y=30}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=450}\\{(1-40%)y-(1-60%)x=30}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=450}\\{40%y-60%x=30}\end{array}\right.$ |
6.若点(3,4)是反比例函数y=$\frac{2m-2}{x}$图象上一点,则此函数图象必须经过点( )
| A. | (2,6) | B. | (2,-6) | C. | (4,-3) | D. | (3,-4) |