题目内容
小华要设计一个摸球游戏,使得摸到红球的概率为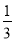
,如果设计符合要求,那么他周末就可以逛公园了,但妈妈对他的设计作出如下要求:(1)至少有四种颜色的球;
(2)至少有一个球是黄球.小华应该怎样设计呢?
答案见解析
【解析】试题分析：用6个球，其中2个红球，1个白球、1个蓝球，2个黄球，从而设计出摸球游戏．
试题解析：【解析】
用6个除颜色外完全相同的红球、白球、蓝球、黄球设计一个摸球游戏，其中2个红球，1个白球、1个蓝球，2个黄球．
作∠AOB的平分线时,以O为圆心,某一长度为半径作弧,与OA,OB分别相交于点C,D,然后分别以点C,D为圆心,适当的长度为半径作弧,使两弧相交于一点,则这个适当的长度为( )
A. 大于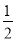
CD B. 等于
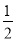CD
C. 小于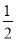
CD D. 以上答案都不对
A
【解析】要保证所作的是角平分线，根据全等三角形的性质，则应再保证两弧相交的点到点C、D的距离相等；画弧时，两弧应有交点才能构成三角形，据此结合三角形的三边关系分析即可．
【解析】
根据三角形两边之和大于第三边的性质可知，
画的时候，为了让两条弧有交点，必须是以大于CD的长为半径画弧．
故选A. 根据所给条件解直角三角形，结果不能确定的是( )
①已知一直角边及其对角；②已知两锐角；③已知斜边和一锐角；④已知一直角边和一斜边；⑤已知直角边和一锐角．
A. ②③ B. ②④ C. 只有② D. ②④⑤
C
【解析】因为解直角三角形，至少已知条件中要给出一条边的长度，所以不能确定的只有②，故选C. 某商场进行有奖促销活动.活动规则:购买500元商品就可以获得一次转转盘的机会(转盘被分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖、纪念奖),转动转盘停止后,指针指在哪个获奖区域就可以获得该区域相应等级奖品一件(奖品设置如图所示).商场工作人员在制作转盘时,将获奖区域扇形圆心角分配如下表:
奖次 | 特等奖 | 一等奖 | 二等奖 | 三等奖 | 纪念奖 |
圆心角 | 1° | 10° | 30° | 90° | 229° |
(1)转动一次转盘,获得圆珠笔的概率是多少?
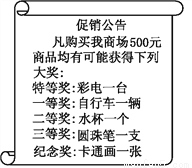
(2)如果不用转盘,请设计一种等效活动方案
(要求写清替代工具和活动规则).
（1） (2)见解析
【解析】试题分析：（1）根据圆珠笔在整个圆中所占的比例即可解答；
（2）根据（1）中所得结果可设计出多种方案，答案不唯一．
试题解析：【解析】
（1）获得圆珠笔的概率为： =；
（2）可采用“抓阄”或“抽签”等方法替代．
在一个不透明的箱子里放进360个除标号不同外，其他均一样的乒乓球，其中一个标“特”、10个标“1”、30个标“2”、90个标... 如图,在4×4正方形网格中,任意选取一个白色的小正方形并涂上阴影,使图中阴影部分的图形构成一个轴对称图形的概率是( )
A.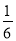 
B. 
C. 
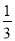D.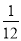 
A
【解析】【解析】
∵白色的小正方形有12个，能构成一个轴对称图形的有2个情况，∴使图中红色部分的图形构成一个轴对称图形的概率是： =．故选A． 用8个除颜色外均相同的球设计一个游戏,使摸到白球与摸不到白球的可能性一样大,摸到红球的可能性比摸到黄球的可能性大,则游戏设计中白、红、黄球的个数可能是( )
A. 4,2,2 B. 3,2,3 C. 4,3,1 D. 5,2,1
C
【解析】【解析】
∵摸到白球与摸不到白球的可能性一样大，摸到红球的可能性比摸到黄球的可能性大，∴白球4个，红球3个，黄球1个．故选C． 如图，沿AC方向开山修路，为了加快施工进度，要在山的另一边同时施工，工人师傅在AC上取一点B，在小山外取一点D，连接BD，并延长使DF=BD，过F点作AB的平行线段MF，连接MD，并延长，在其延长线上取一点E，使DE=DM，在E点开工就能使A、C、E成一条直线，你知道其中的道理吗？
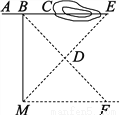
说明见解析
【解析】试题分析：首先证明≌，可得进而得到BE∥MF，再由∥MF根据过直线外一点有且只有一条直线与已知直线平行，可得A、C、E三点在一条直线上．
试题解析：
≌
∴BE∥MF，
∵AB∥MF，
根据过直线外一点有且只有一条直线与已知直线平行，
在一条直线上． 如图，Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC交AD于点E，EF∥AC，下列结论一定成立的是( )
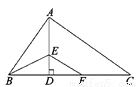
A. AB=BF B. AE=ED
C. AD=DC D. ∠ABE=∠DFE
A
【解析】【解析】
∵∠BAD+∠ABD=90°，∠ABD+∠C=90°
∴∠BAD=∠C（同角的余角相等）
又∵EF∥AC
∴∠BFE=∠C
∴∠BAD=∠BFE
又∵BE平分∠ABC
∴∠ABE=∠FBE
∴∠BEF=∠AEB，
在△ABE与△FBE中，
∠BEF=∠AEB，BE=BE，∠ABE=∠FBE
∴△ABE≌△FB... 已知三边作三角形,用到的基本作图是( )
A. 作一个角等于已知角 B. 作已知直线的垂线
C. 作一条线段等于已知线段 D. 作一条线段等于已知线段的和
C
【解析】已知三角形的三边,求作符合要求的三角形,其作图依据是“SSS”.故用到的基本作图是：作一条线段等于已知线段.
故选C.