��Ŀ����
ij�̳������н������.�����:����500Ԫ��Ʒ�Ϳ��Ի��һ��תת�̵Ļ���(ת�̱���Ϊ5����������,�ֱ����صȽ���һ�Ƚ������Ƚ������Ƚ������),ת��ת��ֹͣ��,ָ��ָ���ĸ�������Ϳ��Ի�ø�������Ӧ�ȼ���Ʒһ��(��Ʒ������ͼ��ʾ).�̳�������Ա������ת��ʱ,������������Բ�ĽǷ������±�:
���� | �صȽ� | һ�Ƚ� | ���Ƚ� | ���Ƚ� | ��� |
Բ�Ľ� | 1�� | 10�� | 30�� | 90�� | 229�� |
(1)ת��һ��ת��,���Բ��ʵĸ����Ƕ���?
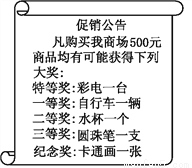
(2)�������ת��,�����һ�ֵ�Ч�����
(Ҫ��д��������ߺͻ����).
 ��1�� (2)������
�������������������1������Բ���������Բ����ռ�ı������ɽ��
��2�����ݣ�1�������ý������Ƴ����ַ������𰸲�Ψһ��
�����������������
��1�����Բ��ʵĸ���Ϊ�� =��
��2���ɲ��á�ץ�Ρ���ǩ���ȷ��������
��һ��������������Ž�360������Ų�ͬ�⣬������һ����ƹ��������һ���ꡰ�ء���10���ꡰ1����30���ꡰ2����90����...
��1�� (2)������
�������������������1������Բ���������Բ����ռ�ı������ɽ��
��2�����ݣ�1�������ý������Ƴ����ַ������𰸲�Ψһ��
�����������������
��1�����Բ��ʵĸ���Ϊ�� =��
��2���ɲ��á�ץ�Ρ���ǩ���ȷ��������
��һ��������������Ž�360������Ų�ͬ�⣬������һ����ƹ��������һ���ꡰ�ء���10���ꡰ1����30���ꡰ2����90����...
 �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д���֪����y�����x�Ĺ�ϵʽΪy��2x��1�����Ա�����( )
A. x B. y C. 2 D. ��1
 A
����������y��2x��1��
���Ա�����x.
��ѡA.
A
����������y��2x��1��
���Ա�����x.
��ѡA. ��ͼ����B��E��C��F��һ��ֱ���ϣ�AB��DE��AB=DE��BE=CF��AC=6����DF=
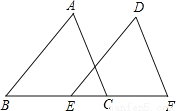
 6.
��������
�����������������������SAS�ɵá�ABC�ա�DEF������ȫ�������ε����ʿɵ�AC=DF=6��
�������: ��AB��DE��
���B=��DEF
��BE=CF��
��BC=EF��
�ڡ�ABC�͡�DEF�У�
��
���ABC�ա�DEF��SAS����
��AC=DF=6��
6.
��������
�����������������������SAS�ɵá�ABC�ա�DEF������ȫ�������ε����ʿɵ�AC=DF=6��
�������: ��AB��DE��
���B=��DEF
��BE=CF��
��BC=EF��
�ڡ�ABC�͡�DEF�У�
��
���ABC�ա�DEF��SAS����
��AC=DF=6�� ��һ�������Ĵ���װ��2������3�������5���������dz���ɫ����������ͬ��
��1�������е���ҡ���Ⱥ���Ӵ����������һ�����ǻ���ĸ��ʣ�
��2�������ٽ����ɸ����������У���ԭ����10������Ȼ����һ��ʹ�Ӵ����������һ�����Ǻ���ĸ�����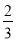 �����������������еĺ���ĸ�����
�����������������еĺ���ĸ�����
 ��1������2��5
��������
�����������1���û���ĸ�������������ĸ���������ø��ʣ�
��2�����ݸ��ʹ�ʽ�г�������ú���ĸ������ɣ�
�����������1���߹�10������2������
��P������
��2������x������������ã�����ã�x=5��
�ʺ���������еĺ�����5����
��1������2��5
��������
�����������1���û���ĸ�������������ĸ���������ø��ʣ�
��2�����ݸ��ʹ�ʽ�г�������ú���ĸ������ɣ�
�����������1���߹�10������2������
��P������
��2������x������������ã�����ã�x=5��
�ʺ���������еĺ�����5���� �����¼������ĸ���Ϊ0����(����)
A. ����˶�Աֻ���1��,�����а���
B. ��ȡһ��������x,����|x|��0
C. ��һ��������,ʹ�����ߵij��ֱ�Ϊ8 cm,6 cm,2 cm
D. ����һö�ʵؾ�����������ֱ����1��6�ĵ���������������,����һ��ĵ���Ϊ6
 C
����������������
A��������¼���������0-1֮�䣻
B���DZ�Ȼ�¼�������=1��
C���Dz������¼�������=0��
D��������¼���������0-1֮�䣮
��ѡC��
C
����������������
A��������¼���������0-1֮�䣻
B���DZ�Ȼ�¼�������=1��
C���Dz������¼�������=0��
D��������¼���������0-1֮�䣮
��ѡC�� ��ͼ��һֻ������������ABCD���������У���O�ǶԽ��ߵĽ��㣬��MON=90�㣬OM��ON�ֱ��߶�AB��BC��M��N���㣬������ͣ������Ӱ����ĸ���Ϊ_____��
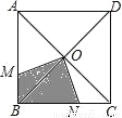
 ��������������������ı���ABCDΪ�����Σ���O�ǶԽ��ߵĽ��㣬
���MBO=��NCO=45�㣬OB=OC����BOC=90�㣬
�ߡ�MON=90�㣬
���MOB+��BON=90�㣬��BON+��NOC=90�㣬
���MOB=��NOC��
�ڡ�MOB�͡�NOC�У��У�
���MOB�ա�NOC��ASA����
ͬ���ɵã���AOM�ա�BON��
��S��Ӱ=S��BOC=...
��������������������ı���ABCDΪ�����Σ���O�ǶԽ��ߵĽ��㣬
���MBO=��NCO=45�㣬OB=OC����BOC=90�㣬
�ߡ�MON=90�㣬
���MOB+��BON=90�㣬��BON+��NOC=90�㣬
���MOB=��NOC��
�ڡ�MOB�͡�NOC�У��У�
���MOB�ա�NOC��ASA����
ͬ���ɵã���AOM�ա�BON��
��S��Ӱ=S��BOC=... С��Ҫ���һ��������Ϸ,ʹ����������ĸ���Ϊ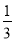 ,�����Ʒ���Ҫ��,��ô����ĩ�Ϳ��Թ乫��,����������������������Ҫ��:(1)������������ɫ����;
,�����Ʒ���Ҫ��,��ô����ĩ�Ϳ��Թ乫��,����������������������Ҫ��:(1)������������ɫ����;
(2)������һ�����ǻ���.С��Ӧ�����������?
 �𰸼�����
�������������������6��������2������1������1������2�����Ӷ���Ƴ�������Ϸ��
�����������������
��6������ɫ����ȫ��ͬ�ĺ��������������һ��������Ϸ������2������1������1������2������
�𰸼�����
�������������������6��������2������1������1������2�����Ӷ���Ƴ�������Ϸ��
�����������������
��6������ɫ����ȫ��ͬ�ĺ��������������һ��������Ϸ������2������1������1������2������ �ڡ�ABC�У�AB=AC=12cm��BC=6cm��DΪBC���е㣬����P��B���������ÿ��1cm���ٶ���B��A��C�ķ����˶������˶�ʱ��Ϊt����ô��t=_________��ʱ����D��P�����ֱ�߽���ABC���ܳ��ֳ��������֣�ʹ����һ��������һ���ֵ�2����
 7��17
����������������������������
��1��P����AB��ʱ����ͼ��
��AB=AC=12cm��BD=CD=BC=��6=3cm��
��P���˶���t�룬��BP=t��AP=12-t��������ã�
BP+BD=��AP+AC+CD����BP+BD��=AP+AC+CD��
��t+3=��12-t+12+3���ٻ�t+3��=12-t+12+3�ڣ�
��ٵ�t=7�룬��ڵã�t=...
7��17
����������������������������
��1��P����AB��ʱ����ͼ��
��AB=AC=12cm��BD=CD=BC=��6=3cm��
��P���˶���t�룬��BP=t��AP=12-t��������ã�
BP+BD=��AP+AC+CD����BP+BD��=AP+AC+CD��
��t+3=��12-t+12+3���ٻ�t+3��=12-t+12+3�ڣ�
��ٵ�t=7�룬��ڵã�t=... �ò���ʽ��ʾͼ�еĽ⼯��������ȷ����( )
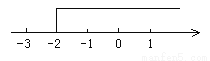
A. x�ݣ�2 B. x����2 C. x����2 D. x�ܣ�2
 A
��������
������������ݲ���ʽ�Ľ⼯�������ϱ�ʾ�����ķ������ɵõ����.
�ò���ʽ��ʾͼ�еĽ⼯Ϊx�ݣ�2����ѡA.
A
��������
������������ݲ���ʽ�Ľ⼯�������ϱ�ʾ�����ķ������ɵõ����.
�ò���ʽ��ʾͼ�еĽ⼯Ϊx�ݣ�2����ѡA. 
