题目内容
根据所给条件解直角三角形，结果不能确定的是( )
①已知一直角边及其对角；②已知两锐角；③已知斜边和一锐角；④已知一直角边和一斜边；⑤已知直角边和一锐角．
A. ②③ B. ②④ C. 只有② D. ②④⑤
C
【解析】因为解直角三角形，至少已知条件中要给出一条边的长度，所以不能确定的只有②，故选C.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
△ABC中，a、b、c分别是∠A、∠B、∠C的对边，如果a2+b2=c2，那么下列结论正确的是（ ）
A. bcosB=c B. csinA=a C. atanA=b D. tanB＝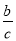
B
【解析】∵a2+b2=c2，
∴△ABC是直角三角形，且∠C=90°，
∴sinA=即csinA=a，
∴B选项正确．
故选B． 计算tan 46°≈_______ ．(精确到0.01)
1.04
【解析】试题解析：tan 46°≈1.0355303138≈1.04.
故答案为：10.4. 如图，点B、E、C、F在一条直线上，AB∥DE，AB=DE，BE=CF，AC=6，则DF=
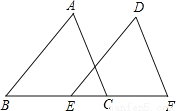
6.
【解析】
试题分析：根据题中条件由SAS可得△ABC≌△DEF，根据全等三角形的性质可得AC=DF=6．
试题解析: ∵AB∥DE，
∴∠B=∠DEF
∵BE=CF，
∴BC=EF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS），
∴AC=DF=6． 在等腰△ABC中，∠A=30°，AB=8，则AB边上的高CD的长是 ．
4或或。
【解析】根据题意画出AB=AC，AB=BC和AC=BC时的图象，然后根据等腰三角形的性质和解直角三角形，分别进行计算即可：
(1)如图，
当AB=AC时，
∵∠A=30°，
∴CD=AC=×8=4。
（2）如图，当AB=BC时，
则∠A=∠ACB=30°。
∴∠ACD=60°。∴∠BCD=30°
∴CD=cos∠BCD•BC=cos3... 在一个不透明的袋中装有2个黄球，3个黑球和5个红球，它们除颜色外其他都相同．
（1）将袋中的球摇均匀后，求从袋中随机摸出一个球是黄球的概率；
（2）现在再将若干个红球放入袋中，与原来的10个球均匀混合在一起，使从袋中随机摸出一个球是红球的概率是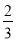
，请求出后来放入袋中的红球的个数．
（1）；（2）5
【解析】
试题分析：（1）用黄球的个数除以所有球的个数即可求得概率；
（2）根据概率公式列出方程求得红球的个数即可．
试题解析：（1）∵共10个球，有2个黄球，
∴P（黄球）；
（2）设有x个红球，根据题意得：，解得：x=5．
故后来放入袋中的红球有5个． 下列事件发生的概率为0的是( )
A. 射击运动员只射击1次,就命中靶心
B. 任取一个有理数x,都有|x|≥0
C. 画一个三角形,使其三边的长分别为8 cm,6 cm,2 cm
D. 拋掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为6
C
【解析】【解析】
A．是随机事件，概率在0-1之间；
B．是必然事件，概率=1；
C．是不可能事件，概率=0；
D．是随机事件，概率在0-1之间．
故选C． 小华要设计一个摸球游戏,使得摸到红球的概率为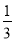
,如果设计符合要求,那么他周末就可以逛公园了,但妈妈对他的设计作出如下要求:(1)至少有四种颜色的球;
(2)至少有一个球是黄球.小华应该怎样设计呢?
答案见解析
【解析】试题分析：用6个球，其中2个红球，1个白球、1个蓝球，2个黄球，从而设计出摸球游戏．
试题解析：【解析】
用6个除颜色外完全相同的红球、白球、蓝球、黄球设计一个摸球游戏，其中2个红球，1个白球、1个蓝球，2个黄球． 一种饮料重约300g，罐上注有“蛋白质含量≥0.5%”，其中蛋白质的含量为多少克？
不少于1.5克
【解析】
试题分析：根据“蛋白质含量≥0.5%”，即可得到结果.
300×0.5%=1.5克
答：其中蛋白质的含量不少于1.5克.