题目内容
18. 如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=2,则CF=4.
如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=2,则CF=4.
分析 根据角平分线的定义得到∠ABO=∠CBO;由平行线的性质得到∠EOB=∠OBC,等量代换得到∠EOB=∠EBO,根据等腰三角形的判定得到BE=OE;同理可证CF=OF;于是得到结论.
解答 解:∵BO平分∠ABC,
∴∠ABO=∠CBO;
∵EO∥BC,
∴∠EOB=∠OBC,
∴∠EOB=∠EBO,
∴BE=OE;
同理可证CF=OF;
∵EF=6,BE=2,
∴OF=EF-OE=EF-BE=4,
∴CF=OF=4,
故答案为:4.
点评 本题考查了角平分线的定义、平行线的性质以及等腰三角形的判定;证明三角形是等腰三角形是解题的关键.

练习册系列答案
相关题目
9.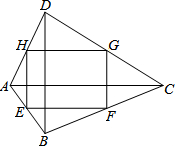 如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )
如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )
 如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )
如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )| A. | 四边形EFGH是矩形 | B. | 四边形EFGH的周长是7 | ||
| C. | 四边形EFGH的面积是24 | D. | 四边形ABCD的面积是48 |
13. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )| A. | ∠A=∠D | B. | AC=BD | C. | ∠ACB=∠DBC | D. | AB=DC |
8.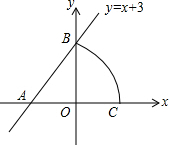 如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )
如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )
 如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )
如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )| A. | (3$\sqrt{2}$-3,0) | B. | (3$\sqrt{2}$,0) | C. | (0,3$\sqrt{2}$-3) | D. | (3,0) |
 如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
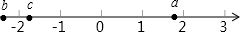 实数a、b、c在数轴上的对应点如图所示,其中|a|=|c|,化简|b+$\sqrt{3}$|+|a-$\sqrt{2}$|+|c-$\sqrt{2}$|+2c.
实数a、b、c在数轴上的对应点如图所示,其中|a|=|c|,化简|b+$\sqrt{3}$|+|a-$\sqrt{2}$|+|c-$\sqrt{2}$|+2c.