题目内容
9.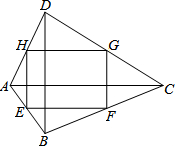 如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )
如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )| A. | 四边形EFGH是矩形 | B. | 四边形EFGH的周长是7 | ||
| C. | 四边形EFGH的面积是24 | D. | 四边形ABCD的面积是48 |
分析 利用三角形的中位线定理证得四边形EFGH为平行四边形,然后利用有一个角是直角的平行四边形是矩形可判断选项A是否正确;由AC=8,BD=6,且AC⊥BD,可求出四边形EFGH和ABCD的面积,由此可判断选项CD是否正确;题目给出的数据求不出四边形EFGH的周长,所以选项B错误.
解答 解:
∵点E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF=$\frac{1}{2}$AC,GH=$\frac{1}{2}$AC,
∴EF=GH,同理EH=FG
∴四边形EFGH是平行四边形;
又∵对角线AC、BD互相垂直,
∴EF与FG垂直.
∴四边形EFGH是矩形,故选项A正确,符合题意;
∵AC=8,BD=6,且AC⊥BD,
∴四边形ABCD的面积=$\frac{1}{2}$AC•BD=24,故选项D错误,不符合题意;
∵四边形EFGH是矩形,且HG=$\frac{1}{2}$AC=4,HE=$\frac{1}{2}$BD=3
∴四边形EFGH的面积=3×4=12,故选项C错误,不符合题意;
∵EF=$\frac{1}{2}$AC=4,HE=$\frac{1}{2}$BD=3,
∴四边形EFGH的周长=2(3+4)=14,所以选项B错误,不符合题意,
故选A.
点评 本题考查了中点四边形的知识,解题的关键是灵活运用三角形的中位线定理,平行四边形的判断及矩形的判断进行证明,是一道综合题.

练习册系列答案
相关题目
17. 所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式.心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质.我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如图表:
所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式.心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质.我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如图表:
四种气质类型人数频数分布表
根据以上信息完成下列问题并补全频数分布直方图:
(1)a=0.36,b=100
(2)请你估计一下,高三年级1200名学生中,胆汁型和多血质的共有多少人?
 所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式.心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质.我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如图表:
所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式.心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质.我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如图表:四种气质类型人数频数分布表
| 气质类型 | 频数 | 频率 |
| 胆汁型 | 180 | a |
| 多血质 | 140 | 0.28 |
| 黏液质 | 80 | 0.16 |
| 抑郁质 | b | 0.20 |
(1)a=0.36,b=100
(2)请你估计一下,高三年级1200名学生中,胆汁型和多血质的共有多少人?
14.化简m+n-(m-n)的结果为( )
| A. | 2m | B. | 2n | C. | 0 | D. | -2n |
1.小明同学买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的5元纸币为x张,根据题意,下面所列方程正确的是( )
| A. | x+5(x-12)=48 | B. | x+5(12-x)=48 | C. | 5x+12(x-5)=48 | D. | 5x+(12-x)=48 |
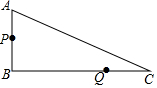 如图,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.点P从点A沿AB方向以1cm/s的速度运动至点B,点Q从点B沿BC方向以6cm/s的速度运动至点C,P、Q两点同时出发.
如图,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.点P从点A沿AB方向以1cm/s的速度运动至点B,点Q从点B沿BC方向以6cm/s的速度运动至点C,P、Q两点同时出发. 如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=2,则CF=4.
如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=2,则CF=4.