题目内容
8.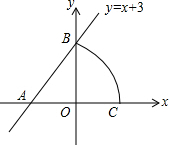 如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )
如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )| A. | (3$\sqrt{2}$-3,0) | B. | (3$\sqrt{2}$,0) | C. | (0,3$\sqrt{2}$-3) | D. | (3,0) |
分析 先根据坐标轴上点的坐标特征得到A(-3,0),B(0,3),再利用勾股定理计算出AB=23$\sqrt{2}$,然后根据圆的半径相等得到AC=AB=3$\sqrt{2}$,进而解答即可.
解答 解:当y=0时,x+3=0,解得x=-3,则A(-3,0);
当x=0时,y=x+3=3,则B(0,3),
所以AB=3$\sqrt{2}$,
因为以点A为圆心,AB为半径画弧,交x轴于点C,
所以AC=AB=3$\sqrt{2}$,
所以OC=AC-AO=3$\sqrt{2}$-3,
所以的C的坐标为(3$\sqrt{2}$-3,0),
故选A.
点评 本题考查了一次函数图象上点的坐标特征,关键是根据一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.

练习册系列答案
相关题目
1.小明同学买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的5元纸币为x张,根据题意,下面所列方程正确的是( )
| A. | x+5(x-12)=48 | B. | x+5(12-x)=48 | C. | 5x+12(x-5)=48 | D. | 5x+(12-x)=48 |
17.点P(1,-2)关于x轴的对称点是P1,P1的坐标为( )
| A. | (1,-2) | B. | (-1,2) | C. | (1,2) | D. | (-2,-1) |
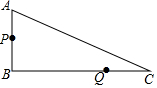 如图,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.点P从点A沿AB方向以1cm/s的速度运动至点B,点Q从点B沿BC方向以6cm/s的速度运动至点C,P、Q两点同时出发.
如图,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.点P从点A沿AB方向以1cm/s的速度运动至点B,点Q从点B沿BC方向以6cm/s的速度运动至点C,P、Q两点同时出发. 如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=2,则CF=4.
如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=2,则CF=4.
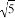 +1 B. -
+1 B. -
 如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PD⊥AB,垂足为D,射线DP交$\widehat{AC}$于点E,交过点C的切线于点F.
如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PD⊥AB,垂足为D,射线DP交$\widehat{AC}$于点E,交过点C的切线于点F.