题目内容
14.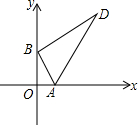 Rt△ABD的两顶点A、B分别在x轴和y轴上运动,其中∠ABD=90°,∠D=30°,AB=4,则顶点D到原点O的距离的最小值为2$\sqrt{13}$-2,顶点D到原点O的距离的最大值为2$\sqrt{13}$+2.
Rt△ABD的两顶点A、B分别在x轴和y轴上运动,其中∠ABD=90°,∠D=30°,AB=4,则顶点D到原点O的距离的最小值为2$\sqrt{13}$-2,顶点D到原点O的距离的最大值为2$\sqrt{13}$+2.
分析 要求OD的最小值和最大值,关键是作出合适的图形,然后根据三角形三边的关系可知两边之差小于第三边,两边之和大约第三边,由勾股定理和在直角三角形中,30°角所对的直角边等于斜边的一半,可以求得BD、BC的长,从而可以求得OD的最小值和最大值,本题得以解决.
解答 解:取AB的中点C,连接OC、CD、OD,如下图所示,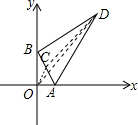
∵∠ABD=90°,∠D=30°,AB=4,
∴AD=8,OC=BC=AC=2,BD=$\frac{AB}{tan30°}$=$\frac{4}{\frac{\sqrt{3}}{3}}$=4$\sqrt{3}$,
∴CD=$\sqrt{B{D}^{2}+B{C}^{2}}$=$\sqrt{(4\sqrt{3})^{2}+{2}^{2}}$=2$\sqrt{13}$,
∴CD-OC≤OD≤CD≤CD+OC,
∴2$\sqrt{13}$-2≤OD≤2$\sqrt{13}$+2.
∴则顶点D到原点O的距离的最小值为2$\sqrt{13}$-2,顶点D到原点O的距离的最大值为2$\sqrt{13}$+2.
故答案为:2$\sqrt{13}$-2,2$\sqrt{13}$+2.
点评 本题考查勾股定理、坐标与图形的性质、直角三角形斜边上的中线等于斜边的一半,直角三角形中30°角所对的直角边与斜边的关系,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
12.若使分式$\frac{x}{x-2}$有意义,则x的取值范围是( )
| A. | x≠2 | B. | x≠-2 | C. | x≠-1 | D. | x=2 |
2.规定★为:x★y=$\frac{1}{xy}+\frac{1}{(x+1)(y+A)}$.已知2★1=$\frac{2}{3}$,则25★26的值为( )
| A. | $-\frac{2}{675}$ | B. | $\frac{4}{675}$ | C. | $\frac{2}{675}$或-$\frac{2}{675}$ | D. | $\frac{2}{675}$ |
9.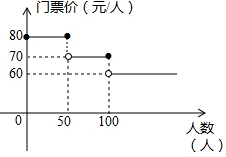 某中学七年级组织学生进行春游,景点门票价格情况如图,则下列说法正确的是( )
某中学七年级组织学生进行春游,景点门票价格情况如图,则下列说法正确的是( )
 某中学七年级组织学生进行春游,景点门票价格情况如图,则下列说法正确的是( )
某中学七年级组织学生进行春游,景点门票价格情况如图,则下列说法正确的是( )| A. | 当旅游人数为50时,则门票价格为70元/人 | |
| B. | 当旅游人数为50或者100的时,门票价格都是70元/人 | |
| C. | 两个班级都是40名学生,则两个班联合起来购票比分别购票要便宜 | |
| D. | 当人数增多时,虽然门票价格越来越低,但是购票总费用会越来越高 |
19.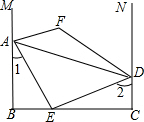 如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F.∠F的度数为( )
如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F.∠F的度数为( )
 如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F.∠F的度数为( )
如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F.∠F的度数为( )| A. | 120° | B. | 135° | C. | 150° | D. | 不能确定 |
3. 如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )
如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )
 如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )
如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | $\frac{AP}{AB}$=$\frac{AB}{AC}$ | D. | $\frac{AB}{AP}$=$\frac{CB}{BP}$ |
4.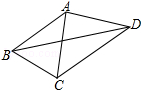 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )度.
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )度.
 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )度.
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )度.| A. | 56 | B. | 78 | C. | 84 | D. | 112 |
