题目内容
2．规定★为：x★y=$\frac{1}{xy}+\frac{1}{（x+1）（y+A）}$．已知2★1=$\frac{2}{3}$，则25★26的值为（ ）| A． | $-\frac{2}{675}$ | B． | $\frac{4}{675}$ | C． | $\frac{2}{675}$或-$\frac{2}{675}$ | D． | $\frac{2}{675}$ |
分析 根据题意可列出方程求出A的值，最后代入求值即可．
解答 解：由题意可知：2★1=$\frac{2}{3}$，
∴$\frac{1}{1×2}$+$\frac{1}{（2+1）•（1+A）}$=$\frac{2}{3}$
解得：A=1
∴25★26=$\frac{1}{25×26}$+$\frac{1}{（25+1）×（26+1）}$=$\frac{2}{675}$
故选（D）
点评 本题考查分式的方程的解法，涉及新定义型运算，代入求值等问题，解题的关键是列出方程求出A的值．
练习册系列答案
相关题目
20．
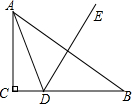如图，在Rt△ABC中，∠ACB=90°，若△ACD的周长为50，DE为AB的垂直平分线，则AC+BC=（ ）
如图，在Rt△ABC中，∠ACB=90°，若△ACD的周长为50，DE为AB的垂直平分线，则AC+BC=（ ）| A． | 25cm | B． | 45cm | C． | 50cm | D． | 55cm |
1．已知x2yn与-xmy3是同类项，则m+n=（ ）
| A． | 5 | B． | 2 | C． | 3 | D． | 1 |
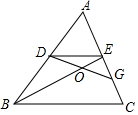如图，在△ABC中，点D，E分别是边AB，AC的中点，点G是EC的中点，连接DG交BE于点O，若△ADE的面积为S，求四边形BDGC的面积．
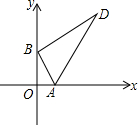Rt△ABD的两顶点A、B分别在x轴和y轴上运动，其中∠ABD=90°，∠D=30°，AB=4，则顶点D到原点O的距离的最小值为2$\sqrt{13}$-2，顶点D到原点O的距离的最大值为2$\sqrt{13}$+2．
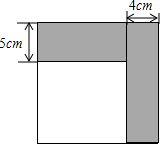如图所示，小明将一张正方形纸片剪去一条宽为4cm的长条后，再从剩下的长方形纸片上剪去一条宽为5cm的长条．如果两次剪下的长条面积正好相等．