题目内容
3. 如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )
如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | $\frac{AP}{AB}$=$\frac{AB}{AC}$ | D. | $\frac{AB}{AP}$=$\frac{CB}{BP}$ |
分析 根据相似三角形的判定方法,逐项判断即可.
解答 解:
∵在△ABP和△ACB中,∠BAP=∠CAB,
∴当∠ABP=∠C时,满足两组角对应相等,可判断△ABP∽△ACB,故A正确;
当∠APB=∠ABC时,满足两组角对应相等,可判断△ABP∽△ACB,故B正确;
当$\frac{AP}{AB}$=$\frac{AB}{AC}$时,满足两边对应成比例且夹角相等,可判断△ABP∽△ACB,故C正确;
当$\frac{AB}{AP}$=$\frac{CB}{BP}$时,其夹角不相等,则不能判断△ABP∽△ACB,故D不正确;
故选D.
点评 本题主要考查相似三角形的判定,掌握相似三角形的判定方法是解题的关键,即在两个三角形中,满足三边对应成比例、两边对应成比例且夹角相等或两组角对应相等,则这两个三角形相似.

练习册系列答案
相关题目
1.已知x2yn与-xmy3是同类项,则m+n=( )
| A. | 5 | B. | 2 | C. | 3 | D. | 1 |
18.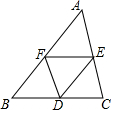 如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
 如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )| A. | △BDF | B. | △DEF | C. | △CDE | D. | △BDF和△CDE |
13.下列各个图中,一定全等的是( )
| A. | 各有一个角是45°的两个等腰三角形 | |
| B. | 两个等边三角形 | |
| C. | 各有一个角是45°,腰长都是3cm的两个等腰三角形 | |
| D. | 腰和顶角对应相等的两个等腰三角形 |
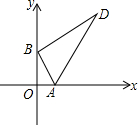 Rt△ABD的两顶点A、B分别在x轴和y轴上运动,其中∠ABD=90°,∠D=30°,AB=4,则顶点D到原点O的距离的最小值为2$\sqrt{13}$-2,顶点D到原点O的距离的最大值为2$\sqrt{13}$+2.
Rt△ABD的两顶点A、B分别在x轴和y轴上运动,其中∠ABD=90°,∠D=30°,AB=4,则顶点D到原点O的距离的最小值为2$\sqrt{13}$-2,顶点D到原点O的距离的最大值为2$\sqrt{13}$+2.
 如图是一个育苗棚,棚宽a=12m,棚高b=5m,棚长d=10m,则覆盖在棚斜面上的塑料薄膜的面积为130m2.
如图是一个育苗棚,棚宽a=12m,棚高b=5m,棚长d=10m,则覆盖在棚斜面上的塑料薄膜的面积为130m2.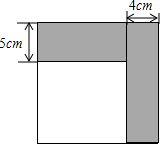 如图所示,小明将一张正方形纸片剪去一条宽为4cm的长条后,再从剩下的长方形纸片上剪去一条宽为5cm的长条.如果两次剪下的长条面积正好相等.
如图所示,小明将一张正方形纸片剪去一条宽为4cm的长条后,再从剩下的长方形纸片上剪去一条宽为5cm的长条.如果两次剪下的长条面积正好相等.