题目内容
5.设a1,a2,…,a10是从1,0,-1这三个数中取值的一列数,若a1+a2+…+a10=1,(a1+1)2+(a2+1)2+…+(a10+1)2=17,则a1,a2,…,a10中1的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 首先根据(a1+1)2+(a2+1)2+…+(a10+1)2得到a12+a22+…+a102+12,然后设有x个1,y个-1,z个0,得到方程组$\left\{\begin{array}{l}{x+y+z=10}\\{1•x+(-1)•y+0•z=1}\\{{1}^{2}x+(-1)^{2}y+{0}^{2}z+12=17}\end{array}\right.$,解方程组即可确定正确的答案.
解答 解:(a1+1)2+(a2+1)2+…+(a2014+1)2=a12+a22+…+a102+2(a1+a2+…+a10)+10
=a12+a22+…+a102+2×1+10
=a12+a22+…+a102+12,
设有x个1,y个-1,z个0
∴$\left\{\begin{array}{l}{x+y+z=10}\\{1•x+(-1)•y+0•z=1}\\{{1}^{2}x+(-1)^{2}y+{0}^{2}z+12=17}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=2}\\{z=5}\end{array}\right.$
∴有3个1,2个-1,5个0,
故选:B.
点评 本题考查了数字的变化类问题,解题的关键是对给出的式子进行正确的变形,难度较大.

练习册系列答案
相关题目
17.甲、乙两个学习小组各有4名同学,在某次测验中,他们的得分情况如下表所示:
设两组同学得分的平均数依次为X甲、X乙,得分的方差依次为S2甲、S2乙,则下列关系中完全正确的是( )
| 组员1 | 组员2 | 组员3 | 组员4 | |
| 甲 | 88 | 95 | 97 | 100 |
| 乙 | 90 | 94 | 97 | 99 |
| A. | X甲=X乙,S2甲>S2乙 | B. | X甲=X乙,S2甲<S2乙 | ||
| C. | X甲<X乙,S2甲>S2乙 | D. | X甲<X乙,S2甲<S2乙 |
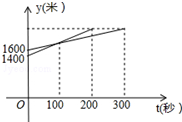 一次越野赛跑中,当甲跑了1600米时,乙跑了1400米,甲、乙在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示:
一次越野赛跑中,当甲跑了1600米时,乙跑了1400米,甲、乙在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示: