题目内容
6.已知a,b,c均为实数,且a>b,c≠0,则下列结论不一定正确的是( )| A. | a+c>b+c | B. | -a<-b | C. | a2>b2 | D. | $\frac{a}{{c}^{2}}$>$\frac{b}{{c}^{2}}$ |
分析 根据不等式的性质1,不等式两边同时加上或减去同一个数,不等号的方向不变;根据不等式的性质2,不等式两边同时乘以或除以同一个正数,不等号的方向不变;根据不等式的性质3,不等式两边同时乘以或除以同一个负数,不等号的方向改变;利用不等式的3个性质进行分析.
解答 解:A、根据不等式的性质一,不等式两边同时加上c,不等号的方向不变,故此选项正确,不合题意;
B、∵a>b,
∴-a<-b,
故此选项正确,不合题意;
C、a2>b2不一定正确,例如:0>-3,而02<(-3)2,符合题意;
D、∵c≠0,
∴c2>0,
∵a>b.
∴$\frac{a}{{c}^{2}}>\frac{b}{{c}^{2}}$,
故此选项正确,不合题意;
故选:C.
点评 本题主要考查了不等式的基本性质.“0”是很特殊的一个数,因此,解答不等式的问题时,应密切关注“0”存在与否,以防掉进“0”的陷阱.
不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
相关题目
17.甲、乙两个学习小组各有4名同学,在某次测验中,他们的得分情况如下表所示:
设两组同学得分的平均数依次为X甲、X乙,得分的方差依次为S2甲、S2乙,则下列关系中完全正确的是( )
| 组员1 | 组员2 | 组员3 | 组员4 | |
| 甲 | 88 | 95 | 97 | 100 |
| 乙 | 90 | 94 | 97 | 99 |
| A. | X甲=X乙,S2甲>S2乙 | B. | X甲=X乙,S2甲<S2乙 | ||
| C. | X甲<X乙,S2甲>S2乙 | D. | X甲<X乙,S2甲<S2乙 |
1.(-2)3的值为( )
| A. | -8 | B. | -6 | C. | 6 | D. | 8 |
10.某学习小组,在探究1+$\frac{2}{x}$的性质时,得到了如下数据:
根据表格中的数据,做出了四个推测:
①1+$\frac{2}{x}$(x>0)的值随着x的增大而减小;
②1+$\frac{2}{x}$(x>0)的值有可能等于1;
③1+$\frac{2}{x}$(x>0)的值随着x的增大越来越接近于1;
④1+$\frac{2}{x}$(x>0)的值最大值是3.则推测正确的有( )
| x | 1 | 10 | 100 | 1000 | 10000 | … |
| 1+$\frac{2}{x}$ | 3 | 1.2 | 1.02 | 1.002 | 1.0002 | … |
①1+$\frac{2}{x}$(x>0)的值随着x的增大而减小;
②1+$\frac{2}{x}$(x>0)的值有可能等于1;
③1+$\frac{2}{x}$(x>0)的值随着x的增大越来越接近于1;
④1+$\frac{2}{x}$(x>0)的值最大值是3.则推测正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
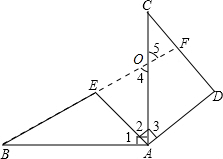 如图,∠BAC=∠DAE=90°,AC=AB,AE=AD,试说明BE⊥CD.
如图,∠BAC=∠DAE=90°,AC=AB,AE=AD,试说明BE⊥CD.