题目内容
15.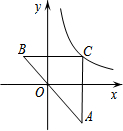 如图,Rt△ABC的斜边AB经过坐标原点,两直角边分别平行于坐标轴,点C在反比例函数$y=\frac{k}{x}$的图象上,若点A的纵坐标为$-\frac{7}{2}$,若点B的横坐标为-2,则k的值为7.
如图,Rt△ABC的斜边AB经过坐标原点,两直角边分别平行于坐标轴,点C在反比例函数$y=\frac{k}{x}$的图象上,若点A的纵坐标为$-\frac{7}{2}$,若点B的横坐标为-2,则k的值为7.
分析 BC与y轴交于点D,AC与x轴交于点E,如图,设C(a,b),证明Rt△BOD∽Rt△OAE,利用相似比得到2:a=b:$\frac{7}{2}$,利用比例性质得到ab=7,然后根据反比例函数图象上点的坐标特征易得k的值.
解答 解:BC与y轴交于点D,AC与x轴交于点E,如图, 设C(a,b),
设C(a,b),
∵点A的纵坐标为$-\frac{7}{2}$,若点B的横坐标为-2,
∴BD=2,AE=$\frac{7}{2}$,
∵∠BOD=∠A,
∴Rt△BOD∽Rt△OAE,
∴BD:OE=OD:AE,即2:a=b:$\frac{7}{2}$,
∴ab=7,
∴C(a,b)在反比例函数$y=\frac{k}{x}$的图象上,
∴k=ab=7.
故答案为7.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
5.如果(2x+y-2)2+|3x-2y-10|=0,那么x和y的值为( )
| A. | x=2,y=2 | B. | x=-2,y=2 | C. | x=-2,y=-2 | D. | x=2,y=-2 |
10.一个圆锥的底面半径为8cm,其侧面展开图的圆心角为240°,则此圆锥的侧面积为( )
| A. | 96πcm2 | B. | 48πcm2 | C. | 36πcm2 | D. | 24πcm2 |
4.正比例函数y=-2x与反比例函数y=$\frac{k}{x}$的图象相交于A(m,2),B两点.则点B的坐标是( )
| A. | (-2,1) | B. | (1,-2) | C. | (-1,2) | D. | (2,-1) |