题目内容
5.先化简,再求值:(1+$\frac{1}{x}$)•$\frac{x}{{x}^{2}-1}$,其中x=$\sqrt{5}$+1.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入原式进行计算即可.
解答 解:原式=$\frac{x+1}{x}$•$\frac{x}{(x+1)(x-1)}$
=$\frac{1}{x-1}$,
当x=$\sqrt{5}$+1时,原式=$\frac{1}{\sqrt{5}+1-1}$=$\frac{\sqrt{5}}{5}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
若A(m,y),B(m-1,y2)两点都在该函数的图象上,当m满足范围m<$\frac{5}{2}$时,y1<y2.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
17.-6的倒数是( )
| A. | 6 | B. | $\frac{1}{6}$ | C. | -$\frac{1}{6}$ | D. | -6 |
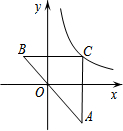 如图,Rt△ABC的斜边AB经过坐标原点,两直角边分别平行于坐标轴,点C在反比例函数$y=\frac{k}{x}$的图象上,若点A的纵坐标为$-\frac{7}{2}$,若点B的横坐标为-2,则k的值为7.
如图,Rt△ABC的斜边AB经过坐标原点,两直角边分别平行于坐标轴,点C在反比例函数$y=\frac{k}{x}$的图象上,若点A的纵坐标为$-\frac{7}{2}$,若点B的横坐标为-2,则k的值为7. 如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=50°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米)
如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=50°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米) 如图所示,与∠1是同位角的个数有2个,并在图中标出.
如图所示,与∠1是同位角的个数有2个,并在图中标出.