题目内容
12．
如图，已知梯形．（1）如果A（-1，3），那么请你分别写出点B，C，D的坐标；
（2）试求梯形ABCD的面积．
分析 （1）由点A的坐标以及B，C，D所在象限的位置即可得到各自的坐标；
（2）由图形的面积公式计算即可．
解答 解：
（1）∵四边形ABCD是梯形，
∴AD∥BC，
∵A（-1，3），
∴B（-2，-1），C（4，-1），D（2，3）；
（2）由图形可知AD=3，BC=6，AD和BC之间的距离为4，
所以梯形的面积=$\frac{（3+6）×4}{2}$=18．
点评 本题考查了梯形的性质坐标与图形的性质以及梯形的面积公式运用，当图形中一些点的坐标求面积时，过已知点向坐标轴作垂线，然后求出相关的线段长，是解决这类问题的基本方法和规律．
练习册系列答案
计算高手系列答案
相关题目
2．
如图，在△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE，PF分别交AB，AC于点E，F，连接EF交AP于点G，给出以下五个结论：
①∠B=∠C=45°；
②AE=CF，
③AP=EF，
④△EPF是等腰直角三角形，
⑤四边形AEPF的面积是△ABC面积的一半．
其中正确的结论是（ ）
如图，在△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE，PF分别交AB，AC于点E，F，连接EF交AP于点G，给出以下五个结论：①∠B=∠C=45°；
②AE=CF，
③AP=EF，
④△EPF是等腰直角三角形，
⑤四边形AEPF的面积是△ABC面积的一半．
其中正确的结论是（ ）
| A． | 只有① | B． | ①②④ | C． | ①②③④ | D． | ①②④⑤ |
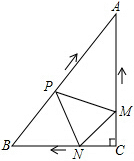如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm，动点M、N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A、B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM，PN，MN，设移动时间为t（单位：秒，0＜t＜2.5）．
17．若分式$\frac{1}{x-2}$有意义，则x的取值范围是（ ）
| A． | x＞2 | B． | x＜2 | C． | x≠2 | D． | x≠0 |
4．“x与5的差的一半是正数”，用不等式可表示为（ ）
| A． | x-$\frac{5}{2}$＞0 | B． | $\frac{x-5}{2}$＞0 | C． | $\frac{x-5}{2}$≥0 | D． | $\frac{x}{2}$-5≥0 |
