题目内容
14.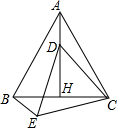 如图,等边△ABC中,AH⊥BC于点H,点D是AB上任意一点,以CD为边作等边△CDE,连结BE.
如图,等边△ABC中,AH⊥BC于点H,点D是AB上任意一点,以CD为边作等边△CDE,连结BE.(1)求证:BE⊥AB;
(2)当点E在AH的延长线上时,试求$\frac{AD}{AH}$的值.
分析 (1)由等边三角形的性质可得出AC=BC、DC=EC,根据角与角之间的关系可得出∠ECB=∠DCA,从而可证出△ACD≌△BCE(SAS),根据全等三角形的性质可得∠EBC=∠DAC,再由AH⊥BC可得出∠DAC=30°,进而即可求出∠EBA=90°,即BE⊥AB;
(2)根据等边三角形的对称轴可得BE=CE,进而可得出∠EBC=∠ECB=∠BCD=∠ACD=30°,即点D是△ABC的内心,也是重心,由此可求出$\frac{AD}{AH}$的值.
解答 (1)证明:∵△DCE与△ABC都是等边三角形,如图1,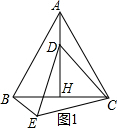
∴∠ACD+∠DCB=∠ACB=60°,∠DCB+∠BCE=∠DCE=60°,AC=BC,DC=EC,
∴∠ECB=∠DCA.
在△ACD和△BCE中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=EC}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠EBC=∠DAC.
又∵AH⊥BC,
∴∠DAC=$\frac{1}{2}$∠BAC=30°,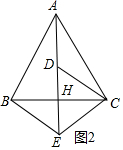
∴∠EBA=∠EBC+∠CBA=90°,即BE⊥AB.
(2)解:当点E在AH的延长线上时,如图2所示.
由等边三角形对称性可得:BE=CE,
∴∠EBC=∠ECB=∠BCD=∠ACD=30°,
∴点D是△ABC的内心,也是重心,
∴$\frac{AD}{AH}$=$\frac{2}{3}$.
点评 本题考查全等三角形的判定与性质、等边三角形的性质以及三角形的重心,解题的关键是:(1)求出∠EBA=90°;(2)找出点D为等边三角形的重心.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
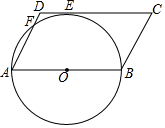 如图,以?ABCD的边AB为直径作⊙O,边CD与⊙O相切于点E,边AD与⊙O相交于点F,已知AB=12,∠C=60°
如图,以?ABCD的边AB为直径作⊙O,边CD与⊙O相切于点E,边AD与⊙O相交于点F,已知AB=12,∠C=60°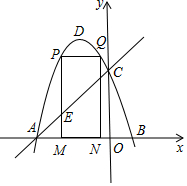 如图,抛物线y=-x2-2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点. 如图,E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE=22.5°.
如图,E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE=22.5°.