题目内容
5.用配方法解方程:2x2+5x+3=0.分析 将常数项移到等式右边,再将二次项系数化为1,继而配上一次项系数的一半的平方,从而得解.
解答 解:∵2x2+5x=-3,
∴x2+$\frac{5}{2}$x=-$\frac{3}{2}$,
∴x2+$\frac{5}{2}$x+$\frac{25}{16}$=-$\frac{3}{2}$+$\frac{25}{16}$,即(x+$\frac{5}{4}$)2=$\frac{1}{16}$,
则x+$\frac{5}{4}$=±$\frac{1}{4}$,
∴x1=-1,x2=-$\frac{3}{2}$.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
相关题目
20.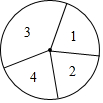 如图是一个转盘,扇形1,2,3的圆心角分别是60°,70°,150°,任意转动转盘,指针指向扇形4的概率是( )
如图是一个转盘,扇形1,2,3的圆心角分别是60°,70°,150°,任意转动转盘,指针指向扇形4的概率是( )
 如图是一个转盘,扇形1,2,3的圆心角分别是60°,70°,150°,任意转动转盘,指针指向扇形4的概率是( )
如图是一个转盘,扇形1,2,3的圆心角分别是60°,70°,150°,任意转动转盘,指针指向扇形4的概率是( )| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
10.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小丽做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如由你摸球一次,你摸到白球的概率P(摸到白球)=0.6;
(3)盒子中有黑球16个.
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如由你摸球一次,你摸到白球的概率P(摸到白球)=0.6;
(3)盒子中有黑球16个.
17.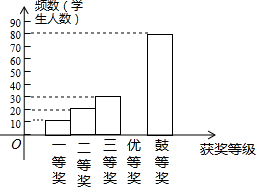 为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
请根据所给信息,解答下列问题:
(1)a=60,b=0.15,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)若我市初中生共有16000人,竞赛活动获奖率为40%,获三等奖以上的学生表示对“足球比较喜欢”,请你估计我市初中生对“足球比较喜欢”的有多少人?
 为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:| 获奖等次 | 频数 | 频率 |
| 一等奖 | 10 | 0.05 |
| 二等奖 | 20 | 0.10 |
| 三等奖 | 30 | b |
| 优胜奖 | a | 0.30 |
| 鼓励奖 | 80 | 0.40 |
(1)a=60,b=0.15,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)若我市初中生共有16000人,竞赛活动获奖率为40%,获三等奖以上的学生表示对“足球比较喜欢”,请你估计我市初中生对“足球比较喜欢”的有多少人?
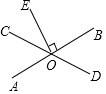 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=40°,求∠AOD的度数.
如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=40°,求∠AOD的度数.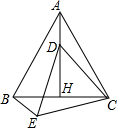 如图,等边△ABC中,AH⊥BC于点H,点D是AB上任意一点,以CD为边作等边△CDE,连结BE.
如图,等边△ABC中,AH⊥BC于点H,点D是AB上任意一点,以CD为边作等边△CDE,连结BE.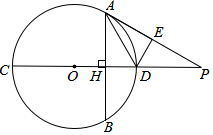 如图,CD为⊙O的直径,弦AB垂直于CD,垂足为H,∠EAD=∠HAD.
如图,CD为⊙O的直径,弦AB垂直于CD,垂足为H,∠EAD=∠HAD.