题目内容
4.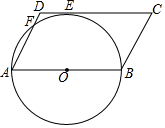 如图,以?ABCD的边AB为直径作⊙O,边CD与⊙O相切于点E,边AD与⊙O相交于点F,已知AB=12,∠C=60°
如图,以?ABCD的边AB为直径作⊙O,边CD与⊙O相切于点E,边AD与⊙O相交于点F,已知AB=12,∠C=60°(1)求弧EF的长;
(2)线段CE的长为2$\sqrt{3}$+6.
分析 (1)首先证明△AOF是等边三角形.求出扇形的圆心角∠EOF即可解决问题.
(2)作BM⊥CD于M.易证四边形OEMB是正方形,OE=EM=BM=OB=6,在Rt△CBM中,求出CM即可.
解答 解:(1)如图,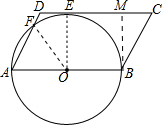 连接OF、OE.
连接OF、OE.
∵四边形ABCD是平行四边形,
∴∠A=∠C=60°,CD∥AB,
∵OA=OF,
∴△AOF是等边三角形,
∴∠AOF=60°,
∵CD是⊙O切线,
∴OE⊥CD,∵CD∥AB,
∴OE⊥AB,
∴∠AOE=90°,
∴∠EOF=30°,
∴$\widehat{EF}$的长为$\frac{30•π•6}{180}$=π.
(2)作BM⊥CD于M.易证四边形OEMB是正方形,OE=EM=BM=OB=6,
在Rt△CBM中,∵∠C=60°,BM=6,
∴tan60°=$\frac{BM}{CM}$,
∴$\sqrt{3}$=$\frac{6}{CM}$,
∴CM=2$\sqrt{3}$,
∴CE=CM+EM=2$\sqrt{3}$+6,
故答案为2$\sqrt{3}$+6.
点评 本题考查切线的性质、平行四边形的性质、等边三角形的判定和性质、扇形的面积公式、解直角三角形等知识,解题的关键是学会添加常用辅助线,灵活运用知识解决问题,属于中考常考题型.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
14.在一次游戏当中,小明将下面四张扑克牌中的三张旋转了180°,得到的图案和原来的一模一样,小芳看了后,很快知道没有旋转那张扑克牌是( )
| A. |  黑桃Q | B. |  梅花2 | C. |  梅花6 | D. |  方块9 |
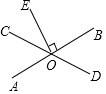 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=40°,求∠AOD的度数.
如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=40°,求∠AOD的度数.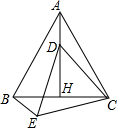 如图,等边△ABC中,AH⊥BC于点H,点D是AB上任意一点,以CD为边作等边△CDE,连结BE.
如图,等边△ABC中,AH⊥BC于点H,点D是AB上任意一点,以CD为边作等边△CDE,连结BE.