题目内容
11.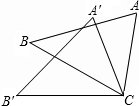 如图,△ABC≌△A'CB′,∠BCB'=32°,则∠ACA′的度数为32°.
如图,△ABC≌△A'CB′,∠BCB'=32°,则∠ACA′的度数为32°.
分析 根据全等三角形对应角相等可得∠ACB=∠A′C′B′,然后求出∠ACA=∠BCB'.
解答 解:∵△ABC≌△A'CB,
∴∠ACB=∠A′CB′,
∴∠ACB-∠A′CB=∠A′CB′-∠A′CB,
即∠ACA′=∠BCB',
∵∠BCB'=32°,
∴∠ACA的度数为32°.
故答案为:32°.
点评 本题考查了全等三角形对应角相等的性质,熟记性质并求出∠ACA=∠BCB'是解题的关键.

练习册系列答案
相关题目
6.下面的几何图形:

其中既是轴对称图形又是中心对称图形的共有( )

其中既是轴对称图形又是中心对称图形的共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
3.已知∠AOB=60°,作射线OC,使∠AOC等于40°,OD是∠BOC的平分线,那么∠BOD的度数是( )
| A. | 100° | B. | 100°或20° | C. | 50° | D. | 50°或10° |
1.顺次连结四边形四条边的中点,所得的四边形是矩形,则原四边形一定是( )
| A. | 平行四边形 | B. | 对角线互相垂直的四边形 | ||
| C. | 菱形 | D. | 对角线相等的四边形 |

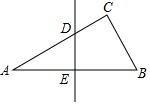 如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=1,求AC的长.
如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=1,求AC的长.