题目内容
20．（1）如图1，已知∠AOB=90°，∠BOC=30°，OM、ON分别平分∠AOC、∠BOC，则∠MON=60°；（2）如图2，已知∠AOB=90°，∠BOC=2x°，OM、ON分别平分∠AOC、∠BOC，求∠BON的度数；
（3）如图3，∠AOB=α，∠BOC=β，仍然有OM，ON分别平分∠AOC、∠BOC，求∠MON．
分析 （1）根据OM、ON分别平分∠AOC、∠BOC可知：∠MON=$\frac{1}{2}$（∠AOB+∠BOC）=$\frac{1}{2}$∠AOC
（2）根据ON平分∠BOC，可知∠BON=$\frac{1}{2}$∠BOC=x°；
（3）根据OM、ON分别平分∠AOC、∠BOC可知：∠MON=$\frac{1}{2}$（∠AOB+∠BOC）=$\frac{1}{2}$（α+β）
解答 解：（1）∠AOC=∠AOB+∠BOC=120°
∵OM、ON分别平分∠AOC、∠BOC，
∴∠MOB=$\frac{1}{2}$∠AOB，∠BON=$\frac{1}{2}$∠BOC，
∴∠MON=∠MOB+∠BON=$\frac{1}{2}$（∠AOB+∠BOC）=$\frac{1}{2}$∠AOC=60°；
（2）∵ON平分∠BOC，
∴∠BON=$\frac{1}{2}$∠BOC=x°；
（3）∵OM、ON分别平分∠AOC、∠BOC，
∴∠MOB=$\frac{1}{2}$∠AOB，∠BON=$\frac{1}{2}$∠BOC，
∴∠MON=∠MOB+∠BON=$\frac{1}{2}$（∠AOB+∠BOC）=$\frac{1}{2}$（α+β）
点评 本题考查角度计算问题，涉及角平分线的性质，属于基础题型．
练习册系列答案
相关题目
小芳和小琦玩抽水果卡片的游戏，有四张如图所示的水果卡片（其中两张草莓图片和两张梨图片，卡片背面完全相同）把背面朝上，洗匀放好，小芳从中随机抽取一张，不放回，小琦再从剩下的三张卡片中随机抽取一张．若两人抽到同一种水果卡片，小芳获胜，否则，小琦获胜．
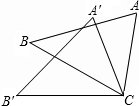如图，△ABC≌△A'CB′，∠BCB'=32°，则∠ACA′的度数为32°．
如图是一个运算程序，若输入x的值为8，输出的结果是m，若输入x的值为3，输出的结果是n，则m-2n=16．
已知如图，△ABC在平面直角坐标系XOY中，其中A（1，2），B（3，1），C（4，3），试解答下列各题：