题目内容
16.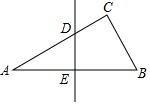 如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=1,求AC的长.
如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=1,求AC的长.
分析 先根据直角三角形的性质求出∠ABC的度数,再由线段垂直平分线的性质得出AD=BD,∠ABD=∠A=30°,故可得出∠DBC=30°,所以BD=2CD=2,由此可得出结论.
解答  解:连接BD,
解:连接BD,
∵在△ABC中,∠C=90°,∠A=30°,
∴∠ABC=60°.
∵AB的垂直平分线DE交AC于D,
∴∠ABD=∠A=30°,
∴∠DBC=30°.
∵CD=1,
∴BD=2CD=2,
∴AD=2,
∴AC=3.
点评 本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )
 有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )| A. | a-b<b-a<0 | B. | b-a<a-b<0 | C. | a-b<0<b | D. | 0<a-b<b |

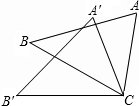 如图,△ABC≌△A'CB′,∠BCB'=32°,则∠ACA′的度数为32°.
如图,△ABC≌△A'CB′,∠BCB'=32°,则∠ACA′的度数为32°.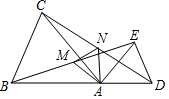 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,M,N分别为BE,CD的中点.
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,M,N分别为BE,CD的中点. 如图是一个运算程序,若输入x的值为8,输出的结果是m,若输入x的值为3,输出的结果是n,则m-2n=16.
如图是一个运算程序,若输入x的值为8,输出的结果是m,若输入x的值为3,输出的结果是n,则m-2n=16. 如图,在平面直角坐标系xOy中,直线y1=kx+m(k≠0)与抛物线y2=ax2+bx+c(a≠0)交于点A(0,4),B(3,1),当 y1≤y2时,x的取值范围是0≤x≤3.
如图,在平面直角坐标系xOy中,直线y1=kx+m(k≠0)与抛物线y2=ax2+bx+c(a≠0)交于点A(0,4),B(3,1),当 y1≤y2时,x的取值范围是0≤x≤3.