题目内容
1.如图,是由边长为1的小正方形构成的网格,各个小正方形的顶点称之为格点,点A、C、E、F均在格点上,根据不同要求,选择格点,画出符合条件的图形:
(1)在图1中,画一个以AC为一边的△ABC,使∠ABC=45°(画出一个即可);
(2)在图2中,画一个以EF为一边的△DEF,使tan∠EDF=$\frac{1}{2}$,并直接写出线段DF的长.
分析 (1)利用网格特点,AB在水平格线上,BC为4×4的正方形的对角线;
(2)由于tan∠EDF=$\frac{1}{2}$,则在含∠D的直角三角形中,满足对边与邻边之比为1:2即可.
解答 解:(1)如图1,△ABC为所作;
(2)如图2,△DEF为所作,DF=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
11.-$\frac{2}{3}$的倒数是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $-\frac{3}{2}$ | D. | $-\frac{2}{3}$ |
16. 如图,已知山坡AB的坡度为1:2,BC=1,则坡长AB=( )
如图,已知山坡AB的坡度为1:2,BC=1,则坡长AB=( )
 如图,已知山坡AB的坡度为1:2,BC=1,则坡长AB=( )
如图,已知山坡AB的坡度为1:2,BC=1,则坡长AB=( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 4 |
 如图,已知BC平分∠DBE,BA分∠DBE成3:4两部分,若∠ABC=8°,求∠DBE的度数.
如图,已知BC平分∠DBE,BA分∠DBE成3:4两部分,若∠ABC=8°,求∠DBE的度数.
 小芳和小琦玩抽水果卡片的游戏,有四张如图所示的水果卡片(其中两张草莓图片和两张梨图片,卡片背面完全相同)把背面朝上,洗匀放好,小芳从中随机抽取一张,不放回,小琦再从剩下的三张卡片中随机抽取一张.若两人抽到同一种水果卡片,小芳获胜,否则,小琦获胜.
小芳和小琦玩抽水果卡片的游戏,有四张如图所示的水果卡片(其中两张草莓图片和两张梨图片,卡片背面完全相同)把背面朝上,洗匀放好,小芳从中随机抽取一张,不放回,小琦再从剩下的三张卡片中随机抽取一张.若两人抽到同一种水果卡片,小芳获胜,否则,小琦获胜.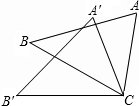 如图,△ABC≌△A'CB′,∠BCB'=32°,则∠ACA′的度数为32°.
如图,△ABC≌△A'CB′,∠BCB'=32°,则∠ACA′的度数为32°.