Question

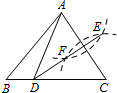
18．如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，点D是AC的中点，连接BD，按以下步骤作图：
①分别以B，D为圆心，大于$\frac{1}{2}$BD的长为半径作弧，两弧相交于点P和点Q；②作直线PQ交AB于点E，交BC于点F，则BF=（　　）

• A． $\frac{5}{6}$
• B． 1
• C． $\frac{13}{6}$
• D． $\frac{5}{2}$

Answer 1

分析 连结DF，利用基本作图得到由EF垂直平分BD，则BF=DF，设BF=x，则DF=x，CF=3-x，然后在Rt△DCF中利用勾股定理得到2²+（3-x）²=x²，然后解方程即可．

解答 解：连结DF，由作法得EF垂直平分BD，则BF=DF，
∵点D是AC的中点，
∴CD=$\frac{1}{2}$AC=2，
设BF=x，则DF=x，CF=3-x，
在Rt△DCF中，2²+（3-x）²=x²，解得x=$\frac{13}{6}$，
即BF=$\frac{13}{6}$．
故选C．

点评 本题考查了作图-基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．也考查了勾股定理．