题目内容
13. 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:①分别以点A、D为圆心,以大于$\frac{1}{2}$AD的长为半径在AD两侧作弧,交于两点M、N;②连接MN分别交AB、AC于点E、F;③连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是( )
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:①分别以点A、D为圆心,以大于$\frac{1}{2}$AD的长为半径在AD两侧作弧,交于两点M、N;②连接MN分别交AB、AC于点E、F;③连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 根据已知得出MN是线段AD的垂直平分线,推出AE=DE,AF=DF,求出DE∥AC,DF∥AE,得出四边形AEDF是菱形,根据菱形的性质得出AE=DE=DF=AF,根据平行线分线段成比例定理得出$\frac{BD}{CD}$=$\frac{BE}{AE}$,代入求出即可.
解答 解:∵根据作法可知:MN是线段AD的垂直平分线,
∴AE=DE,AF=DF,
∴∠EAD=∠EDA,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠EDA=∠CAD,
∴DE∥AC,
同理DF∥AE,
∴四边形AEDF是菱形,
∴AE=DE=DF=AF,
∵AF=4,
∴AE=DE=DF=AF=4,
∵DE∥AC,
∴$\frac{BD}{CD}$=$\frac{BE}{AE}$,
∵BD=6,AE=4,CD=3,
∴$\frac{6}{3}$=$\frac{BE}{4}$,
∴BE=8,
故选D.
点评 本题考查了平行线分线段成比例定理,菱形的性质和判定,线段垂直平分线性质,等腰三角形的性质的应用,能根据定理四边形AEDF是菱形是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例.

练习册系列答案
相关题目
2.为了解学生课外阅读的喜好,某校从六年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计.图(1)与图(2)是整理数据后绘制的两幅不完整的统计图.以下结论不正确的是( )


| A. | 由这两个统计图可知被抽查的学生中,喜欢“科普常识”的学生有90人 | |
| B. | 若该年级共有900名学生,则可估计喜爱“科普常识”的学生约有270人 | |
| C. | 由这两个统计图不能估计喜欢“小说”的人数 | |
| D. | 在扇形统计图中,“漫画”所在扇形的圆心角为72° |
3.下列关于有理数的说法中,错误的是( )
| A. | 所有的整数都是有理数 | B. | 所有的分数都是有理数 | ||
| C. | 所有的无限小数都是有理数 | D. | 所有的有限小数都是有理数 |
18. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:
①分别以B,D为圆心,大于$\frac{1}{2}$BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:①分别以B,D为圆心,大于$\frac{1}{2}$BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
| A. | $\frac{5}{6}$ | B. | 1 | C. | $\frac{13}{6}$ | D. | $\frac{5}{2}$ |
 如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F,当点D从点A运动到点B时,线段EF的最小值是5$\sqrt{3}$.
如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F,当点D从点A运动到点B时,线段EF的最小值是5$\sqrt{3}$.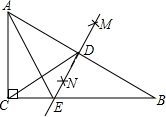 如图,在△ABC中,∠ACB=90°,分别以点A、点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD、AE,请你依作图信息写一个正确的结论AE=BE(答案不唯一).
如图,在△ABC中,∠ACB=90°,分别以点A、点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD、AE,请你依作图信息写一个正确的结论AE=BE(答案不唯一).
 如图所示,在等腰三角形ABC中,AB=AC,若BC=$\sqrt{3}$AB,求∠B的三个三角函数值.
如图所示,在等腰三角形ABC中,AB=AC,若BC=$\sqrt{3}$AB,求∠B的三个三角函数值.