题目内容
3.已知实数x,y满足(x-$\sqrt{{x}^{2}+4}$)(y-$\sqrt{{y}^{2}+2}$)=16,则x$\sqrt{{y}^{2}+2}$+y$\sqrt{{x}^{2}+4}$的值为-$\frac{31}{4}$.分析 原式两边都乘以(x+$\sqrt{{x}^{2}+4}$)(y+$\sqrt{{y}^{2}+2}$)可得(x+$\sqrt{{x}^{2}+4}$)(y+$\sqrt{{y}^{2}+2}$)=$\frac{1}{2}$,展开后可得xy+x$\sqrt{{y}^{2}+2}$+y$\sqrt{{x}^{2}+4}$+$\sqrt{({x}^{2}+4)({y}^{2}+2)}$=$\frac{1}{2}$ ①,再将原式展开后可得xy-x$\sqrt{{y}^{2}+2}$-y$\sqrt{{x}^{2}+4}$+$\sqrt{({x}^{2}+4)({y}^{2}+2)}$=16 ②,①-②即可得答案.
解答 解:∵(x-$\sqrt{{x}^{2}+4}$)(y-$\sqrt{{y}^{2}+2}$)=16,
∴(x-$\sqrt{{x}^{2}+4}$)(y-$\sqrt{{y}^{2}+2}$)(x+$\sqrt{{x}^{2}+4}$)(y+$\sqrt{{y}^{2}+2}$)=16(x+$\sqrt{{x}^{2}+4}$)(y+$\sqrt{{y}^{2}+2}$),
即16(x+$\sqrt{{x}^{2}+4}$)(y+$\sqrt{{y}^{2}+2}$)=8,
∴(x+$\sqrt{{x}^{2}+4}$)(y+$\sqrt{{y}^{2}+2}$)=$\frac{1}{2}$,
xy+x$\sqrt{{y}^{2}+2}$+y$\sqrt{{x}^{2}+4}$+$\sqrt{({x}^{2}+4)({y}^{2}+2)}$=$\frac{1}{2}$ ①,
∵(x-$\sqrt{{x}^{2}+4}$)(y-$\sqrt{{y}^{2}+2}$)=16,
即xy-x$\sqrt{{y}^{2}+2}$-y$\sqrt{{x}^{2}+4}$+$\sqrt{({x}^{2}+4)({y}^{2}+2)}$=16 ②,
∴①-②,得:2x$\sqrt{{y}^{2}+2}$+2y$\sqrt{{x}^{2}+4}$=-$\frac{31}{2}$,
∴x$\sqrt{{y}^{2}+2}$+y$\sqrt{{x}^{2}+4}$=-$\frac{31}{4}$,
故答案为:-$\frac{31}{4}$.
点评 本题考查了二次根式的化简求值,将原式变形得出含有待求代数式的式子是解题的关键.

 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:①分别以B,D为圆心,大于$\frac{1}{2}$BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
| A. | $\frac{5}{6}$ | B. | 1 | C. | $\frac{13}{6}$ | D. | $\frac{5}{2}$ |
| A. | x=1,y=3 | B. | x=4,y=1 | C. | x=3,y=2 | D. | x=2,y=3 |
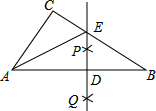 如图,在△ABC中,∠C=90°,∠CAB=62°,按以下步骤作图:
如图,在△ABC中,∠C=90°,∠CAB=62°,按以下步骤作图: