题目内容
16.解下列分式方程:(1)$\frac{x-3}{x-2}$+1=$\frac{3}{2-x}$;
(2)$\frac{x}{2x-3}$+$\frac{5}{3-2x}$=4;
(3)$\frac{x+1}{x-2}$+$\frac{1}{x+1}$=1;
(4)$\frac{5x-4}{x-2}$=$\frac{4x+10}{3x-6}$-1.
分析 (1)首先找出最简公分母,进而去分母解方程得出答案;
(2)首先找出最简公分母,进而去分母解方程得出答案;
(3)首先找出最简公分母,进而去分母解方程得出答案;
(4)首先找出最简公分母,进而去分母解方程得出答案.
解答 解:(1)$\frac{x-3}{x-2}$+1=$\frac{3}{2-x}$
方程两边同乘以x-2得:
x-3+(x-2)=-3,
解得:x=1,
检验:当x=1时,x-2≠0,故分式方程的解为x=1;
(2)$\frac{x}{2x-3}$+$\frac{5}{3-2x}$=4
方程两边同乘以2x-3得:
x-5=4(2x-3),
解得:x=1,
检验:当x=1时,2x-3≠0,故分式方程的解为x=1;
(3)$\frac{x+1}{x-2}$+$\frac{1}{x+1}$=1
方程两边同乘以(x-2)(x+1)得:
(x+1)2+(x-2)=(x-2)(x+1),
解得:x=-$\frac{1}{4}$,
检验:当x=-$\frac{1}{4}$时,(x-2)(x+1)≠0,故分式方程的解为x=-$\frac{1}{4}$;
(4)$\frac{5x-4}{x-2}$=$\frac{4x+10}{3x-6}$-1
方程两边同乘以3(x-2)得:
则3(5x-4)=4x+10-3(x-2),
解得:x=2,
当x=2时,3(x-2)=0,故原方程无解.
点评 此题主要考查了解分式方程,正确找出最简公分母是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.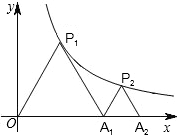 如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
 如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )| A. | -1+$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | -2+2$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
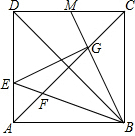 如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.
如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.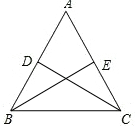 如图,D、E分别是AB、AC的中点,CD⊥AB,垂足为D,BE⊥AC,垂足为E,求证:AC=AB.
如图,D、E分别是AB、AC的中点,CD⊥AB,垂足为D,BE⊥AC,垂足为E,求证:AC=AB.



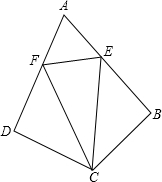 如图,在四边形ABCD中,∠ADC=∠ABC=90°,CB=CD,点E、F分别在AB、AD上,AE=AF,联结CE,CF.
如图,在四边形ABCD中,∠ADC=∠ABC=90°,CB=CD,点E、F分别在AB、AD上,AE=AF,联结CE,CF.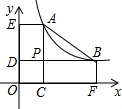 如图,点A,B在双曲线y=$\frac{k}{x}$(x>0)上,分别过点A、B向x轴、y轴作垂线.垂足分别为点C、E、F、D,AC和BD交于点P,$\frac{AP}{PC}$=2且△ABP的面积为4,有以下结论:
如图,点A,B在双曲线y=$\frac{k}{x}$(x>0)上,分别过点A、B向x轴、y轴作垂线.垂足分别为点C、E、F、D,AC和BD交于点P,$\frac{AP}{PC}$=2且△ABP的面积为4,有以下结论: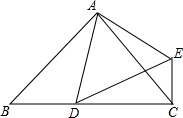 已知:如图,$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$.
已知:如图,$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$.