题目内容
4.已知△ABC中,∠ACB=90°,OD⊥BC,OE⊥AC,OF⊥AB,垂足分别为D,E,F,且OD=OE=OF,FD交直线AC于M.(1)如图1,若点O在△ABC内部,求证:AE+CM=AB;
(2)如图2,若点O在△ABC外部,则(1)中的结论是否仍成立?若成立,请证明;若不成立,请直接写出AE,CM,B三条线段之间的数量关系.
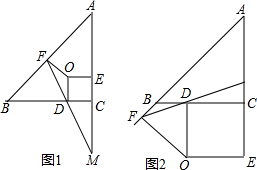
分析 (1)如图1中,连接AO,OB,由△AOF≌△AOE得AF=AE,同理BF=BD,再根据△ODB≌△DCM得BD=CM,由AE+CM=AF+BF=AB得证.
(2)结论:AE-CM=AB,方法类似(1)略.
解答 (1)证明:如图1中,连接AO,OB.
∵OE⊥AC,OF⊥AB,
∴∠AEO=∠AFO=90°,
在RT△AOF和RT△AOE中,
$\left\{\begin{array}{l}{AO=AO}\\{OF=OE}\end{array}\right.$,
∴△AOF≌△AOE,
∴AE=AF,同理BF=BD,
∵OF=OD,BD=BF,
∴BO⊥FD,
∴∠OBD+∠BDF=90°,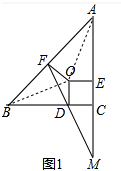
∵∠BDF=∠MDC,∠MDC+∠M=90°,
∴∠M=∠OBD,
∵∠ODC=∠DCE=∠OEC=90°,
∴四边形ODCE是矩形,
∵OE=OD,
∴四边形ODCE是正方形,
∴OD=CD,
在△ODB和△DCM中,
$\left\{\begin{array}{l}{∠OBD=∠M}\\{∠ODB=∠DCM}\\{OD=DC}\end{array}\right.$
∴△ODB≌△DCM,
∴BD=CM,
∴AE+CM=AF+BF=AB.
(2)结论:AE-CM=AB,理由如下:
证明:如图2中,连接AO,OB.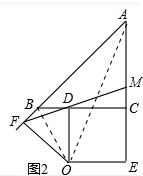
∵OE⊥AC,OF⊥AB,
∴∠AEO=∠AFO=90°,
在RT△AOF和RT△AOE中,
$\left\{\begin{array}{l}{AO=AO}\\{OF=OE}\end{array}\right.$,
∴△AOF≌△AOE,
∴AE=AF,同理BF=BD,
∵OF=OD,BD=BF,
∴BO⊥FD,
∴∠OBD+∠BDF=90°
∵∠BDF=∠MDC,∠MDC+∠CMD=90°,
∴∠CMD=∠OBD,
∵∠ODC=∠DCE=∠OEC=90°,
∴四边形ODCE是矩形,
∵OE=OD,
∴四边形ODCE是正方形,
∴OD=CD,
在△ODB和△DCM中,
$\left\{\begin{array}{l}{∠ODB=∠CMD}\\{∠ODB=∠DCM}\\{OD=DC}\end{array}\right.$,
∴△ODB≌△DCM,
∴BD=CM,
∴AE-CM=AF-BF=AB.
点评 本题考查全等三角形的判定和性质、正方形的判定和性质、正确寻找全等三角形是解题的关键,属于中考常考题型.

| A. | 46.2×1010 | B. | 4.62×1011 | C. | 4.62×1010 | D. | 0.462×1011 |
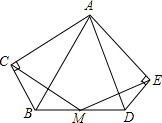 在Rt△ABC和Rt△ADE中,∠BAC=∠DAE,取BD中点M.求证:MC=ME.
在Rt△ABC和Rt△ADE中,∠BAC=∠DAE,取BD中点M.求证:MC=ME.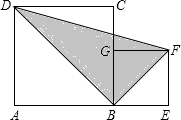 如图,正方形ABCD和正方形BEFG两正方形的面积分别是10和3,那么阴影部分面积是$\sqrt{30}$.
如图,正方形ABCD和正方形BEFG两正方形的面积分别是10和3,那么阴影部分面积是$\sqrt{30}$. 在△ABC中,AB=15,AC=20,∠B-∠C=90°,则线段BC的长度为7.
在△ABC中,AB=15,AC=20,∠B-∠C=90°,则线段BC的长度为7. 如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得出线段BE,连接AE,若AB=2cm,CD=3cm,过B点作BF⊥AB,过点E作EG⊥AB交AB的延长线于点G,试求△ABE的面积.
如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得出线段BE,连接AE,若AB=2cm,CD=3cm,过B点作BF⊥AB,过点E作EG⊥AB交AB的延长线于点G,试求△ABE的面积.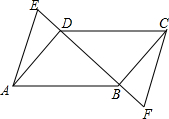 已知,如图,E,D,B,F在同一条直线上,AD∥CB,∠BAD=∠BCD,DE=BF,求证:AE∥CF.
已知,如图,E,D,B,F在同一条直线上,AD∥CB,∠BAD=∠BCD,DE=BF,求证:AE∥CF.