题目内容
1.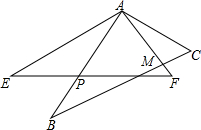 如图,在△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠BAE=24°,∠F=57°,边BC与AF相交于点M,边AB与EF相交于点P.
如图,在△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠BAE=24°,∠F=57°,边BC与AF相交于点M,边AB与EF相交于点P.(1)请说明∠BAE=∠CAF的理由;
(2)△ABC可以经过图形的变换的得到△AEF,请你描述这个变换;
(3)求∠AMB的度数.
分析 (1)若证∠BAE=∠CAF,可证∠BAC=∠EAF,而∠BAC、∠EAF是△ABC和△AEF的俩内角,只需结合题目条件证△ABC≌△AEF可得;
(2)由(1)知△ABC≌△AEF,根据旋转性质可知△ABC绕点A顺时针旋转24°,可以得到△AEF;
(3)∠AMB是△ACM的外角,由(1)知∠BAE=∠CAF、∠C=∠F,即可得∠AMB的度数.
解答 解:(1)在△ABC和△AEF中,
∵$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△AEF(SAS),
∴∠C=∠F,∠BAC=∠EAF,
∴∠BAC-∠PAF=∠EAF-∠PAF,
∴∠BAE=∠CAF=24°;
(2)通过观察可知△ABC绕点A顺时针旋转24°,可以得到△AEF;
(3)由(1)知∠C=∠F=57°,∠BAE=∠CAF=24°,
∴∠AMB=∠C+∠CAF=57°+24°=81°.
点评 本题主要考查全等三角形的判定和性质及旋转变换的性质,结合题意证明两三角形全等是解题关键.

练习册系列答案
相关题目
8.下列条件中,能判定四边形是平行四边形的条件是( )
| A. | 一组对边平行,另一组对边相等 | B. | 一组对边平行,一组对角相等 | ||
| C. | 一组对边平行,一组邻角互补 | D. | 一组对边相等,一组邻角相等 |
13.昌吉赣客运专线是我省第一条南北纵向的高速铁路,设计时速为每小时350公里,总投资约46200000000元.数字46200000000可用科学记数法表示为( )
| A. | 46.2×1010 | B. | 4.62×1011 | C. | 4.62×1010 | D. | 0.462×1011 |
11.一张试卷只有25道选择题,做对一题得4分,做错1题倒扣1分,某学生做了全部试题,得75分,他做对( )题.
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
 如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得出线段BE,连接AE,若AB=2cm,CD=3cm,过B点作BF⊥AB,过点E作EG⊥AB交AB的延长线于点G,试求△ABE的面积.
如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得出线段BE,连接AE,若AB=2cm,CD=3cm,过B点作BF⊥AB,过点E作EG⊥AB交AB的延长线于点G,试求△ABE的面积.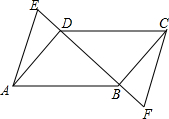 已知,如图,E,D,B,F在同一条直线上,AD∥CB,∠BAD=∠BCD,DE=BF,求证:AE∥CF.
已知,如图,E,D,B,F在同一条直线上,AD∥CB,∠BAD=∠BCD,DE=BF,求证:AE∥CF.