题目内容
15.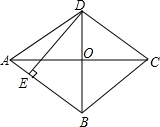 如图,菱形ABCD中,对角线AC、BD相交于点O,DE⊥AB于点E,若菱形的周长为8$\sqrt{13}$,tan∠OAD=$\frac{2}{3}$,求DE的长.
如图,菱形ABCD中,对角线AC、BD相交于点O,DE⊥AB于点E,若菱形的周长为8$\sqrt{13}$,tan∠OAD=$\frac{2}{3}$,求DE的长.
分析 由菱形的周长为8$\sqrt{13}$,tan∠OAD=$\frac{2}{3}$,可求得其边长与对角线的长,然后由菱形的面积等于其对角线积的一半或底乘以高,求得答案.
解答 解:∵菱形ABCD的周长为8$\sqrt{13}$,
∴AD=AB=2$\sqrt{13}$,AC⊥BD,
在Rt△AOD中,tan∠OAD=$\frac{2}{3}$,
∴OD:OA=2:3,
∴设OD=2x,则OA=3x,
在Rt△AOD中,AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=$\sqrt{13}$x,
∴$\sqrt{13}$x=2$\sqrt{13}$,
解得:x=2,
∴OA=6,OD=4,
∴AC=2OA=12,BD=2OD=8,
∵DE⊥AB,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=AB•DE,
∴DE=$\frac{\frac{1}{2}AC•BD}{AB}$=$\frac{24\sqrt{13}}{13}$.
点评 此题考查了菱形的性质以及三角函数等知识.注意菱形的面积等于其对角线积的一半或底乘以高.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
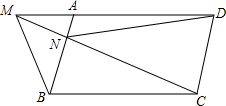 已知M是?ABCD的DA边的延长线上任一点,连结MC交AB于N,求证:S△MNB=S△AND.
已知M是?ABCD的DA边的延长线上任一点,连结MC交AB于N,求证:S△MNB=S△AND.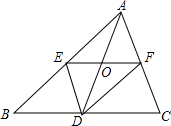 如图,在△ABC中,EF为△ABC的中位线,D为BC边上的中点,AD与EF交于点O,连结EF、DF.求证:四边形AEDF为平行四边形.
如图,在△ABC中,EF为△ABC的中位线,D为BC边上的中点,AD与EF交于点O,连结EF、DF.求证:四边形AEDF为平行四边形.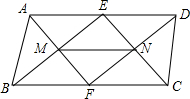 如图所示,已知在?ABCD中,E,F分别是AD,BC的中点,求证:MN∥BC.
如图所示,已知在?ABCD中,E,F分别是AD,BC的中点,求证:MN∥BC.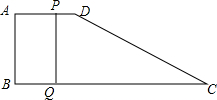 如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=10cm,AB=12cm,BC=18cm,CD=15cm,动点P,Q分别从点A、C同时出发,点P以2cm/s的速度由点A向点B运动,点Q以3cm/s的速度由点C向点B运动.
如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=10cm,AB=12cm,BC=18cm,CD=15cm,动点P,Q分别从点A、C同时出发,点P以2cm/s的速度由点A向点B运动,点Q以3cm/s的速度由点C向点B运动. 八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线,如果一条对角线用了38盆红花,还需要从花房运来多少盆红花?为什么?如果一条对角线用了49盆呢?
八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线,如果一条对角线用了38盆红花,还需要从花房运来多少盆红花?为什么?如果一条对角线用了49盆呢?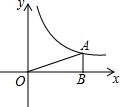 如图,反比例函数y=$\frac{k}{x}$的图象经过点A(4,b).过点A作AB⊥x轴于点B,△AOB的面积为2.求:
如图,反比例函数y=$\frac{k}{x}$的图象经过点A(4,b).过点A作AB⊥x轴于点B,△AOB的面积为2.求: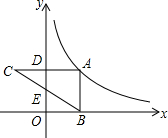 如图,点A在反比例函数y=$\frac{k}{2x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使CD=AD,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为6,则k的值为12.
如图,点A在反比例函数y=$\frac{k}{2x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使CD=AD,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为6,则k的值为12.