题目内容
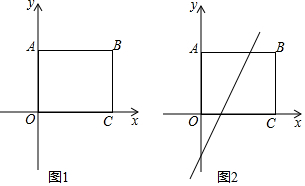
2.方程x2+kx+k-2=0的两根分别为x1,x2,且x1<0<x2<1,则k取值范围是$\frac{1}{2}$<k<2.分析 将一元二次方程的解转化为抛物线与x轴的交点问题,画出函数图象,利用数形结合即可得出关于k的一元一次不等式组,解之即可得出结论.
解答 解:令y=x2+kx+k-2,则点(x1,0)、(x2、0)为抛物线与x轴的交点坐标,
依照题意画出图形,如图所示.
根据题意得:$\left\{\begin{array}{l}{k-2<0}\\{1+k+k-2>0}\end{array}\right.$,
解得:$\frac{1}{2}$<k<2.
故答案为:$\frac{1}{2}$<k<2.
点评 本题考查了抛物线与x轴的交点、二次函数的图象以及解一元一次不等式组,利用数形结合找出关于k的一元一次不等式组是解题的关键.

练习册系列答案
相关题目
12.下列调查中,样本最具有代表性的是( )
| A. | 在重点中学调查全市高一学生的数学水平 | |
| B. | 调查七年级中的两位同学,以了解全校学生的课外辅导用书拥有量 | |
| C. | 为了了解武汉市老人的身体健康状况,选取公园内锻炼的100位老人作调查 | |
| D. | 了解班上学生的睡眠时间,调查班上学号为双的学生的睡眠时间 |
14. 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | ∠2与∠1是同位角 | B. | ∠C与∠1是内错角 | ||
| C. | ∠2与∠3是同旁内角 | D. | ∠B与∠3是同位角 |
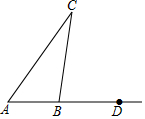 已知:如图所示,在△ABC中,∠A=50°,∠C=30°,点D在射线AB上,请你用量角器过D点画直线DE∥BC,简述你的作法,并说明理由.
已知:如图所示,在△ABC中,∠A=50°,∠C=30°,点D在射线AB上,请你用量角器过D点画直线DE∥BC,简述你的作法,并说明理由.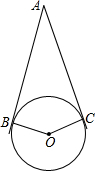 如图,AB、AC与⊙O相切于B、C两点,∠A=40°,点P是圆上异于B、C的一动点,则∠BPC=70或110度.
如图,AB、AC与⊙O相切于B、C两点,∠A=40°,点P是圆上异于B、C的一动点,则∠BPC=70或110度.
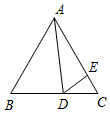 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE=$\frac{4}{3}$,则△ABC的面积为9$\sqrt{3}$.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE=$\frac{4}{3}$,则△ABC的面积为9$\sqrt{3}$.